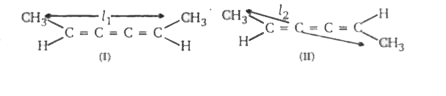
I and II are geometrical isomers of each other because Solution in Telugu
l1=l2
l1>l2
l2>l1
l1andl2 cannot be compared.
The correct Answer is:C
Topper's Solved these Questions
- ISOMERISM (STRUCTURAL & STEREOISOMERISM)BOOK - MS CHOUHANCHAPTER - ISOMERISM (STRUCTURAL & STEREOISOMERISM)EXERCISE - LEVEL 2
66 Videos
- ISOMERISM (STRUCTURAL & STEREOISOMERISM)BOOK - MS CHOUHANCHAPTER - ISOMERISM (STRUCTURAL & STEREOISOMERISM)EXERCISE - LEVEL 2 (SUBJECTIVE PROBLEMS)
17 Videos
- HYDROCARBONS (ALKYNES)BOOK - MS CHOUHANCHAPTER - HYDROCARBONS (ALKYNES)EXERCISE - Level -1
32 Videos
- IUPAC NAME BOOK - MS CHOUHANCHAPTER - IUPAC NAME EXERCISE - LEVEL-2 (SUBJECTIVE PROBLEMS )
1 Videos
Similar Questions
Match the Column (I) and (II).

View SolutionNumber of chiral isomers are:

View SolutionComplete the following reaction

View Solution
When IUPAC name of following compound is given, then double bond and substituent gets respectively (x and y) number so the sum of (x + y) will be
View SolutionStatement-1: The geometrical isomers of the complex [M(NH3)4Cl2] are optically inactive.
Statement-2: Both geometrical isomers of the complex [M[NH3)4Cl2] possess axis of symmetry.
View SolutionStatement I This compound will show geometrical isomerism Statement-II : Terminla carbon groups are perpendicular to each other
View Solution
I and II are grometrical isomers of each other because
View SolutionGeometrical isomers :
View SolutionIsomerism| types of isomers|geometrical isomers|optical isomers
View SolutionA: C_(2)BrCIFI can form 6 different geometrical isomers. R : Each one structure is geometrical isomer of other five structures.
View SolutionAssertion (A) : BrCl+I can form to 6 different geometrical isomers .
Reason (R) : Each one structure is geometrical isomere of other five structures .
View SolutionIdentify the pair of isomers which are geometrical isomers of each.
View SolutionI) (A) and (B) are diastereomers II) (B) and (D) are enantiomers III) (A) and (D) are geometric isomer IV) (A) and ( C ) are optical isomer
View SolutionGeometrical Isomers
View SolutionGeometrical Isomers
View SolutionGeometrical Isomers
View Solution

