If a plot a V vs .∘C at constant pressure is drawn, at what temperatures will it cut the volume and temperature axes?
To solve the problem of determining at what temperatures a plot of volume (V) versus temperature (T) in degrees Celsius (°C) at constant pressure will cut the volume and temperature axes, we can follow these steps:
1. Understand Charles's Law:
Charles's Law states that at constant pressure, the volume (V) of a fixed amount of gas is directly proportional to its absolute temperature (T) in Kelvin. Mathematically, this can be expressed as:
V∝T
or
V=kT
where k is a constant.
2. Convert Temperature to Celsius:
Since we want the temperature in degrees Celsius, we need to relate the Kelvin temperature to Celsius. The relationship is given by:
T(K)=T(°C)+273
Therefore, we can express the volume in terms of Celsius temperature:
V=k(T(°C)+273)
3. Rearranging the Equation:
Rearranging the equation gives us:
V=kT(°C)+273k
This is a linear equation in the form V=mT+b, where m=k and b=273k.
4. Finding the Volume Axis Intercept:
To find where the graph cuts the volume axis (V-axis), we set T(°C)=0:
V=k(0+273)=273k
Thus, the volume intercept is at V=273k.
5. Finding the Temperature Axis Intercept:
To find where the graph cuts the temperature axis (T-axis), we set V=0:
0=k(T(°C)+273)
This implies:
T(°C)+273=0
Therefore:
T(°C)=−273
This indicates that the graph cuts the temperature axis at −273°C.
Summary of Results:
- The graph will cut the volume axis at V=273k (where k is a constant).
- The graph will cut the temperature axis at T=−273°C.
Charles's Law states that at constant pressure, the volume (V) of a fixed amount of gas is directly proportional to its absolute temperature (T) in Kelvin. Mathematically, this can be expressed as:
V∝T
or
V=kT
where k is a constant.
Since we want the temperature in degrees Celsius, we need to relate the Kelvin temperature to Celsius. The relationship is given by:
T(K)=T(°C)+273
Therefore, we can express the volume in terms of Celsius temperature:
V=k(T(°C)+273)
Rearranging the equation gives us:
V=kT(°C)+273k
This is a linear equation in the form V=mT+b, where m=k and b=273k.
To find where the graph cuts the volume axis (V-axis), we set T(°C)=0:
V=k(0+273)=273k
Thus, the volume intercept is at V=273k.
To find where the graph cuts the temperature axis (T-axis), we set V=0:
0=k(T(°C)+273)
This implies:
T(°C)+273=0
Therefore:
T(°C)=−273
This indicates that the graph cuts the temperature axis at −273°C.
- The graph will cut the volume axis at V=273k (where k is a constant).
- The graph will cut the temperature axis at T=−273°C.
Topper's Solved these Questions
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Fill In The Blanks)
25 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Ture False)
25 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Concept Application 5.3
1 Videos
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective
11 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Two gases A and B having the same pressure P, volume V and temperature T are mixed. If mixture has volume and temperature as V and T respectively, then the pressure of the mixture will be
View SolutionA gas is filled in a container of volume V at constant pressure and at 27∘C temperature. Find out the amount of gas that will escape out of the container if temperature rises to 37∘C
View Solution
Knowledge Check
What is the effect on the pressure of a gas if its temperature is increased at constant volume ?
AThe pressure of the gas increases.BThe pressure of the gas decreases .CThe pressure of the gas remains same .DThe pressure of the gas becomes half.Pressure remaining constant, at what temperature the volume of a gas will be double of its volume at 0∘C ?
A100∘CB546∘CC273KD546K
The raise in the temperature of a given mass of an ideal gas at constant pressure and at temperature 27∘ to double its volume is
View SolutionThe volume of a given mass of a gas is 100ml at 100°C. If pressure is kept constant at what temperature will the sample have the volume of 200ml?
View SolutionA quantity of gas occupies an initial volume V0 at pressure p0 and temperature T0. It expands to a volume V (a) constant temperature and (b) constant pressure. In which case does the gas do more work ?

View SolutionAperfect gas at 27∘C is heated at constant pressure soas to duuble its volume. The increase in temperature of the gas will be
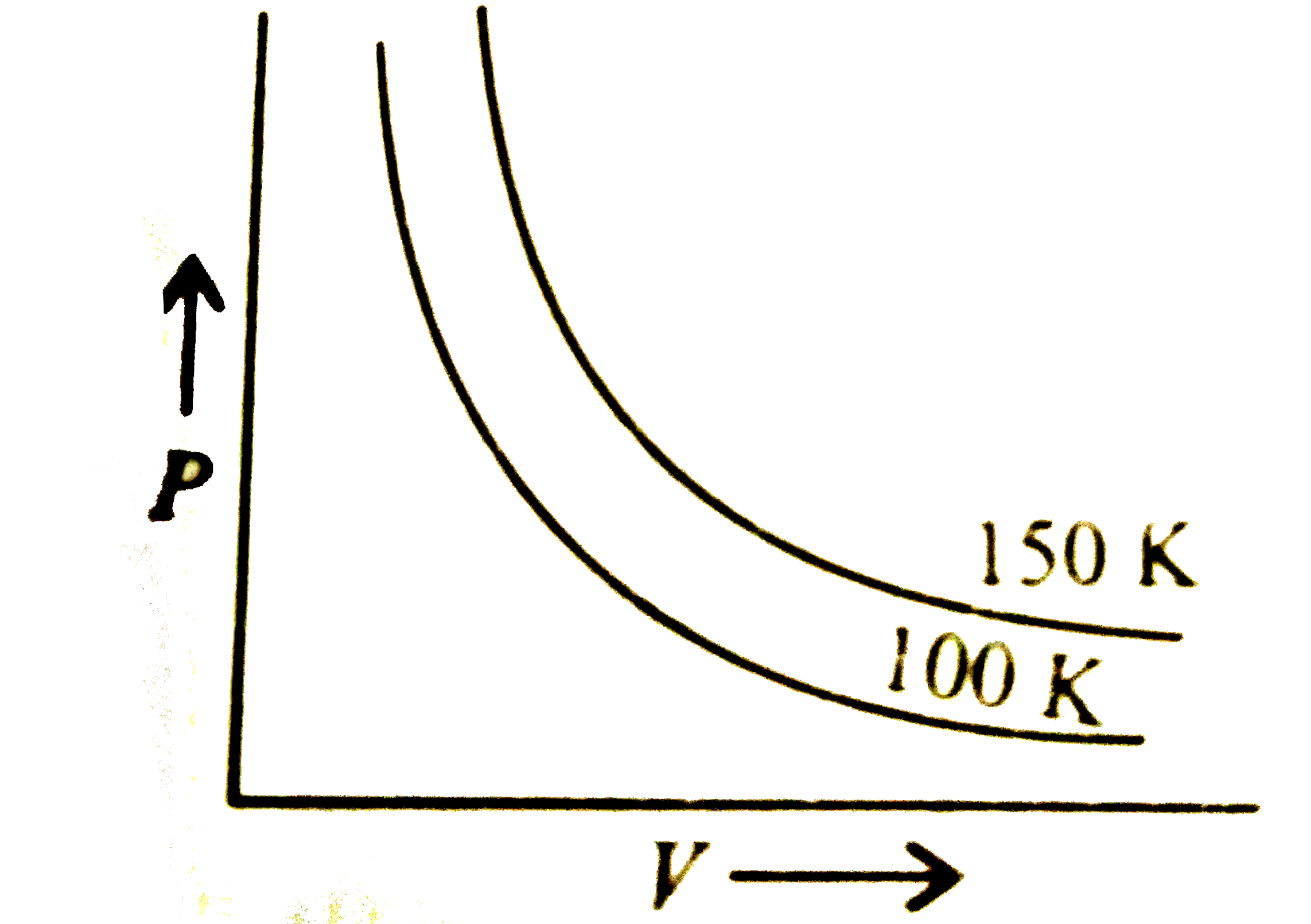
View SolutionA graph is plotted between pressure and volume at different temperatures . On the basis of the graph what changes will you observe in the volume if
(i) the pressure is increased at constant temperature .
(ii) the temperature is decreased at constant pressure .
View SolutionVariation of volume with temperature was first studied by French chemist, Jacques Charles, in 1787 and then extended by another French chemist Joseph Gay-Lussac in 1802. For a fixed mass of a gas under isobaric condition, variation of volume V with temperature t°C is given by V = V0[l+αt] where V0 is the volume at 0°C, at constant pressure.
1 or every 1° change in temperature, the volume of the gas changes by............... of the volume at 0∘ C
View Solution
