In a simple, body-centred and face-centred cubic unit cell, the radii of constituent particles are r1,r2andr3, respectively. If the edge length of each type of these unit cells be a, then find the ratio of r1,r2andr3.Solution in Bengali
For the cubic unit cell, r1=a2,r2=√3a4,r3=a2√2
∴r1:r2:r3=a2:√3a4:a2√2=2:√3:√2
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - SOLID STATEEXERCISE - VERY SHORT ANSWER TYPE60videos
SOLID STATE
- BOOK - CHHAYA PUBLICATIONCHAPTER - SOLID STATEEXERCISE - SOLVED WBCHSE SCANNER8videos
SOLID STATE
- BOOK - CHHAYA PUBLICATIONCHAPTER - SOLID STATEEXERCISE - PRACTICE SET 113videos
SOLID STATE
- BOOK - CHHAYA PUBLICATIONCHAPTER - PREVIOUS YEARS QUESTION PAPER 2019EXERCISE - WBCHSE 2019 PART-B19videos
PREVIOUS YEARS QUESTION PAPER 2019
- BOOK - CHHAYA PUBLICATIONCHAPTER - SOME p-BLOCK ELEMENTSEXERCISE - PRACTIVE SET 1115videos
SOME p-BLOCK ELEMENTS
Similar Questions
What are the constituent particles in a network or covalent solid?
05:06View Solution(i) Which type of semiconductor is sillicon having arsenic as impurity?
(ii) An elements (density = 7.2g⋅cm−3) crystallises in a body-centred cubic structure having its cell edge length 2.88Å. Calculate the number of atoms and the number of unit cells present in 156g of the element.06:33View SolutionThe unit cell with crystallographic dimensions, a≠b≠c,α=γ=90∘,β≠90∘ is-
03:27View SolutionWhich of the following is strongly attracted by magnetic field /
03:05View SolutionHow will you separate CO and CO2 from a mixture?
View SolutionThree circles with centres C_(1),C_(2) and C_(3) and radii r_(1),r_(2) and r_(3) where *r_(-)1
02:49View SolutionFind the currents going through the three resistors R_(v),R_(2)andR_(3) in the circuit of figure.
 07:14View Solution
07:14View SolutionIn CsCl with cubic structure, Cl^(-) ions are located at each corner and Cs^(+) ions at the centre of the unit cell. If r_(Cs^(+)) and r_(Cl^(-)) and 1.69Å and 1.81Å respectively. Find the value of edge length of cube.
08:26View SolutionIn an ionic solid r(+)=1.6A and r(−)=1.864A. Use the radius ratio to determine the edge length of the cubic unit cell in A.
02:30View SolutionIn an ionic solid r_(c)=1.6Å and r_(a)=1.86Å . Find edge length of cubic unit cell is Å
01:13View SolutionAn ionic compound is expected to have body centred type cubic unit cell if rc/ra:
05:03View SolutionDetermine the ratio of radii of particles in simple, body-centred and face-centred cubic unit cells. Assume the edge length of each type of unit cell is a.
01:54View SolutionIf radii of particles in simple cubic, body-centred cubic and face-centred cubic unit cell are r_(1),r_(2),andr_(3) respectively, and each of this unit cell has an edge length of 0.16nm, then the ratio of r_(1),r_(2),andr_(3) is-
02:55View SolutionIf the polynomials f(x)=x4−aandg(x)=a−x4 be divided by x and -x respectively, the respective remainders are r1andr2. Also if r1−r2=0, find the value of a.
03:51View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can
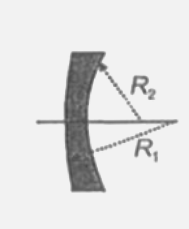 02:33View Solution
02:33View Solution

