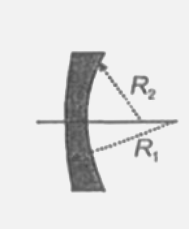
If R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can
Correct myopia
Correct hypermetropia
Correct presbiopia
Correct astigmatism
The correct Answer is:A
Step by step video & image solution for If R_(1)andR_(2) are the radii of curvature of the spherical surfaces of a thin lens and R_(1)gtR_(2), then this lens can by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTECHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - D)
16 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTECHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - B)
30 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
All questions refer to the diagram given below. The denoted lines represent the two surfaces of a lens that may be plane or curved. R1 and R2 are the radii of curvature of the surfaces on the left and right respectively. The refractive index of the medium to the left of the lens is n1, that of the material of the lens itself is n2, and that of the medium to the lens is n3. The first and second focal lengths of the lens are f1 and f2 respectively.
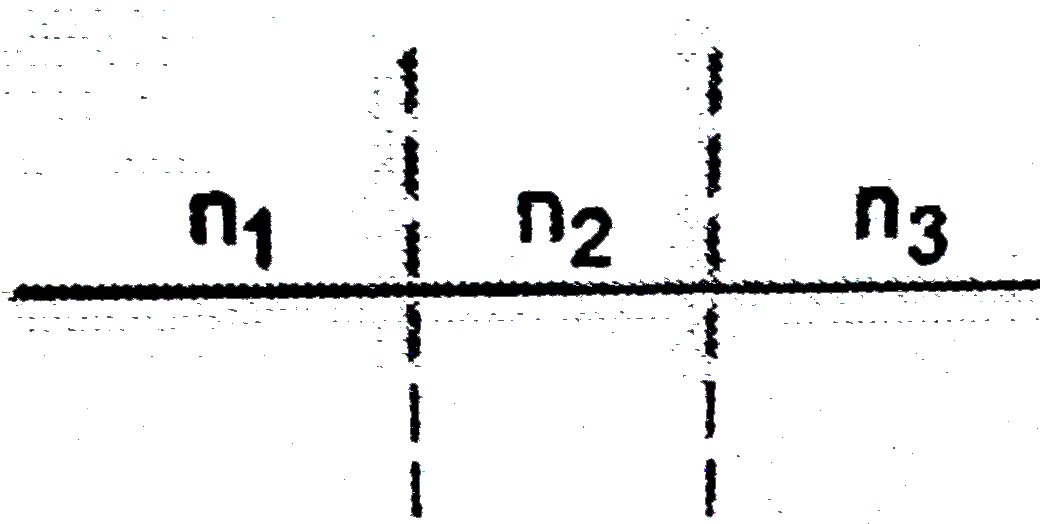
Column A contains certain conditions and column B contains some results which may follow from such conditions.
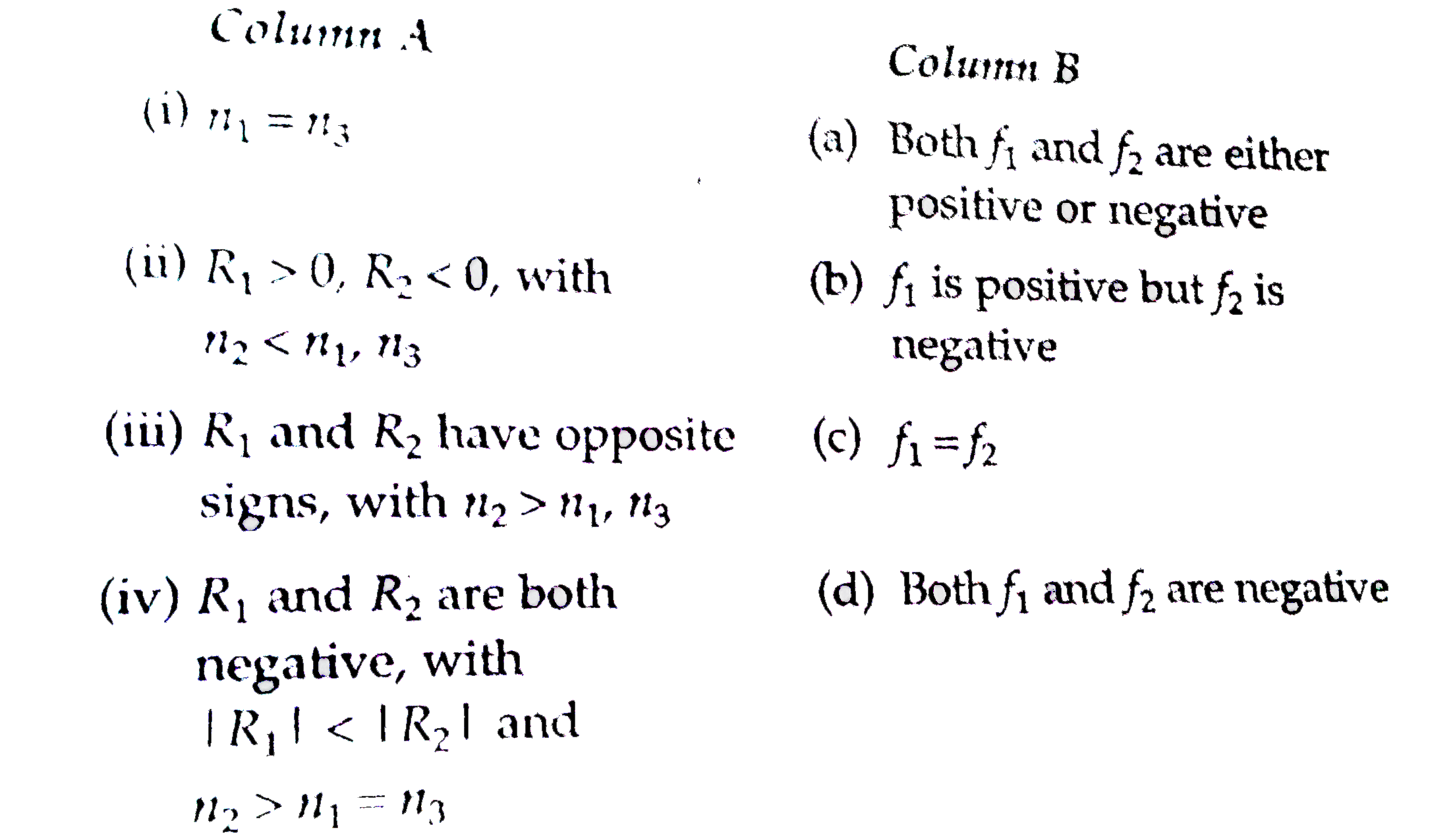
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
Let the given biconvex lens be divided in two equal parts, as shown in Fig. (a), along a section YY' which is perpendicular to the principal axis of lens. What is the power of each part?

View Solution
Knowledge Check
If R1 and R2 are the radii of curvature of double convex lens made of same material, the lens with more focal length is
AR1=20cm,R2=10cmBR1=R2=20cmCR1=R2=10cmDR1=R2=5cmIf R1 and R2 are the radii of curvature of a double convex lens. The largest power will be for
AR1=∞,R2=10cmBR1=10cm,R2=∞CR1=10cm,R2=10cmDR1=5cm,R2=5cmA thin plano-convex lens fits exactly into a thin plano-concave lens. Their plane surfaces are parallel to each other. The lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surfaces of the lenses, if rays are incident parallel to principal axis on lens of refractive index.
Aμ1 then the focal length of the combination is Rμ1−μ2Bμ2 then the focal length of combination is 2Rμ2μ1Cμ1 then the focal length of the combination is R2(μ1−μ2)Dμ2 then the focal length of the combination is R(μ2−μ1)
Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is your answer modified if the given biconvex lens is divided into two parts along a section XX' along its principal axis ?
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If two lens parts obtained in (b) are joined together as shown in Fig. (c), (i) what is the net power of the combination?
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is result of part (d) modified if two parts are placed together as shown in Fig. (c)(ii)?
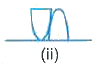
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If twoplanoconvex lenses fromed as a result of (a) are joined together as shown in Fig. (b), what is the net power of the combination ?
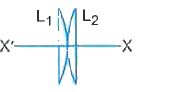
View SolutionSpherical Surface||Refraction and thin Lens
View Solution