In an hcp structure, calculate
Zeff
To calculate the effective number of atoms per unit cell (Z_eff) in a hexagonal close-packed (hcp) structure, we need to consider the contributions from the corner atoms, face-centered atoms, and the atoms in the body of the unit cell.
1. Identify the Atoms in the HCP Structure:
- In an hcp structure, there are:
- 12 corner atoms
- 2 face-centered atoms
- 3 atoms in the body (side body) of the unit cell
2. Calculate Contribution from Corner Atoms:
- Each corner atom is shared among 6 unit cells.
- Therefore, the contribution from the corner atoms is:
Contribution from corner atoms=12×16=2
3. Calculate Contribution from Face-Centered Atoms:
- Each face-centered atom is shared between 2 unit cells.
- Therefore, the contribution from the face-centered atoms is:
Contribution from face-centered atoms=2×12=1
4. Calculate Contribution from Atoms in the Body:
- The 3 atoms in the side body are not shared and belong entirely to the unit cell.
- Therefore, the contribution from these atoms is:
Contribution from side body atoms=3×1=3
5. Sum Up All Contributions:
- Now, we add all the contributions together to find Z_eff:
Zeff=Contribution from corner atoms+Contribution from face-centered atoms+Contribution from side body atoms
Zeff=2+1+3=6
Final Answer:
The effective number of atoms per unit cell (Z_eff) in an hcp structure is 6.
- In an hcp structure, there are:
- 12 corner atoms
- 2 face-centered atoms
- 3 atoms in the body (side body) of the unit cell
- Each corner atom is shared among 6 unit cells.
- Therefore, the contribution from the corner atoms is:
Contribution from corner atoms=12×16=2
- Each face-centered atom is shared between 2 unit cells.
- Therefore, the contribution from the face-centered atoms is:
Contribution from face-centered atoms=2×12=1
- The 3 atoms in the side body are not shared and belong entirely to the unit cell.
- Therefore, the contribution from these atoms is:
Contribution from side body atoms=3×1=3
- Now, we add all the contributions together to find Z_eff:
Zeff=Contribution from corner atoms+Contribution from face-centered atoms+Contribution from side body atoms
Zeff=2+1+3=6
The effective number of atoms per unit cell (Z_eff) in an hcp structure is 6.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - NCERT Exercise104videos
NCERT BASED EXERCISE
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Short Answer Type Questions(ElectroCHMmical Cell)4videos
NCERT BASED EXERCISE
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - NCERT Exerise25videos
NCERT BASED EXERCISE
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - GRIGNARD REAGENTS AND ORGANOMETALLIC REAGENTSEXERCISE - Exercises Archives (Linked Comprehension)1videos
GRIGNARD REAGENTS AND ORGANOMETALLIC REAGENTS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Archives Subjective13videos
NUCLEAR CHEMISTRY
Similar Questions
In a diamond cubic (dc) structure, calculate
ZeffView SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body centre and at the edge centre of the cube.
a. Celculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.View SolutionIn a CCP structure, calculate the minimum distance between two tetrahedral voids.
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and Y atoms are at the face centres. One atoms X is misssing from the corner.
a. Calculate (i). Zeff' (ii). total number of the atoms in the cube, and (iii). formula of the compound.
b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corners of the cube of and two atoms (Y) are at each body diagonal of the cube.
a. Calculate: (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all atoms form one body diagonal of the cube except corners are removed, calculate: (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.View SolutionIf the total number of atoms per unit cell in an hcp structure and a bcc structure gets halved, then ratio of percentage voids in hcp and bcc structures is
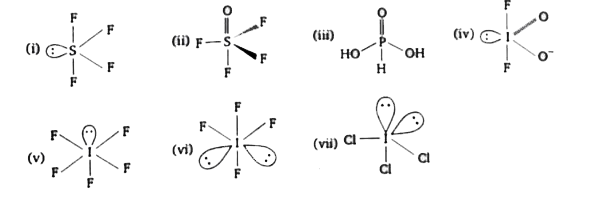
View SolutionConsider the following structures and calculate value of (P2−Q2)
Where P=total number of correct structure representation.
Q=Total number of incorrect structure representation.
 View Solution
View SolutionWhich has hcp crystal structure ?
View SolutionWhich has hcp crystal structure ?
View SolutionAccording to Slater's rule , correct order of Zeff on valence shell electron is :
View Solution

