Name the types of interaction or intermolecular forces of which potential energy-distance function are given below
(a) E∝1r (b) E∝1r2 (c ) E∝1r3
(d) E∝1r4 (e) E∝1r6 .
To solve the problem, we will analyze each potential energy-distance function provided and identify the corresponding type of intermolecular force or interaction.
1. Identify the first potential energy function:
- Given: E∝1r
- This function is characteristic of ionic interactions. Ionic interactions occur between charged ions, where the potential energy decreases with increasing distance.
2. Identify the second potential energy function:
- Given: E∝1r2
- This function corresponds to ion-dipole interactions. These interactions occur between an ion and a polar molecule (dipole), where the potential energy decreases with the square of the distance.
3. Identify the third potential energy function:
- Given: E∝1r3
- This function is associated with dipole-dipole interactions. These interactions occur between two polar molecules, where the potential energy decreases with the cube of the distance.
4. Identify the fourth potential energy function:
- Given: E∝1r4
- This function is indicative of ion-induced dipole interactions. These occur when an ion induces a dipole in a neutral molecule, and the potential energy decreases with the fourth power of the distance.
5. Identify the fifth potential energy function:
- Given: E∝1r6
- This function is characteristic of London dispersion forces (also known as induced dipole-induced dipole interactions). These forces arise due to temporary fluctuations in electron density in atoms or non-polar molecules, and the potential energy decreases with the sixth power of the distance.
Summary of Intermolecular Forces:
- (a) E∝1r - Ionic interactions
- (b) E∝1r2 - Ion-dipole interactions
- (c) E∝1r3 - Dipole-dipole interactions
- (d) E∝1r4 - Ion-induced dipole interactions
- (e) E∝1r6 - London dispersion forces
- Given: E∝1r
- This function is characteristic of ionic interactions. Ionic interactions occur between charged ions, where the potential energy decreases with increasing distance.
- Given: E∝1r2
- This function corresponds to ion-dipole interactions. These interactions occur between an ion and a polar molecule (dipole), where the potential energy decreases with the square of the distance.
- Given: E∝1r3
- This function is associated with dipole-dipole interactions. These interactions occur between two polar molecules, where the potential energy decreases with the cube of the distance.
- Given: E∝1r4
- This function is indicative of ion-induced dipole interactions. These occur when an ion induces a dipole in a neutral molecule, and the potential energy decreases with the fourth power of the distance.
- Given: E∝1r6
- This function is characteristic of London dispersion forces (also known as induced dipole-induced dipole interactions). These forces arise due to temporary fluctuations in electron density in atoms or non-polar molecules, and the potential energy decreases with the sixth power of the distance.
- (a) E∝1r - Ionic interactions
- (b) E∝1r2 - Ion-dipole interactions
- (c) E∝1r3 - Dipole-dipole interactions
- (d) E∝1r4 - Ion-induced dipole interactions
- (e) E∝1r6 - London dispersion forces
Topper's Solved these Questions
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Exercises Linked Comprehension
43 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Exercises Multiple Correct(Chemical Bonding )
7 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Ex 2 .2 Subjective (Molecular Orbital Theory)
4 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Concept Applicationexercise(4.3)
19 Videos
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Subjective type
1 Videos
Similar Questions
Which of the following intermolecular forces have a potential energy distance function as E∝1r2
(i) Ion -dipole (ii) Dipole -dipole (iii) Ion -induced dipole (iv) London dispersion forces .
View SolutionMatch the type of interaction in column A with the distance dependence of their interaction energy in column B :
AB(I)ion-ion(a)1r(II)dipole-dipole(b)1r2(III)London dispersion(c)1r3(d)1r6
View Solution
Knowledge Check
Assertion : For a first order reaction,t1/2 is indepent of rate constant.
Reason : For a first reaction t1/2∝[R]0.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Column I shows charge distribution and column II shows electrostatic field created by that charge at a point r distance from its centre.
(,Column I ,,Column II),((A),A stationary point charge,(p),E∝r0),((B),A stationary uniformly long charge rod,(q),E∝r1),((C),A stationary electric dipole,(r),E∝r⋅−1),,(s),E∝r−2),(,,(t),E∝r−3):}
View SolutionThe electirc potential between a proton and an electron is given by V=V0ln(rr0) , where r_0 is a constant. Assuming Bhor model to be applicable, write variation of rn with n, being the principal quantum number. (a) rn∝n (b) rn∝1n (c ) r2n (d)rn∝1n2
View SolutionDraw E-r and V-r graphs due to two charged spherical shells as shown in figure (along the line between C and ∝)

View SolutionStudy the graph given below and choose the option that is correctly describing the relationship between dissolved oxygen (DO) and biochemical oxygen demand (BOD) :
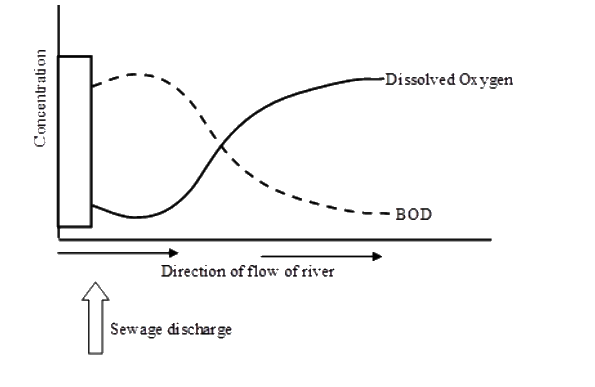
(a) DO∝3BOD
(b) DO∝2BOD
(c) DO∝1BOD
(d) DO∝BOD
View SolutionFor x∈R, limx→∞(x−3x+2)x is equal to (a) e (b) e−1 (c) e−5 (d) e5
View SolutionAssume that the force of gravitation F∝1rn . Then show that the orbital speed in a circular orbit of radius r is proportional to 1r(n−1)/2 , while its period T is proportional to r(n+1)/2
View SolutionIn the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
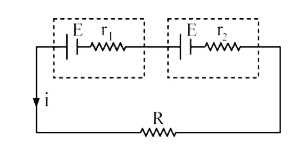
View Solution
