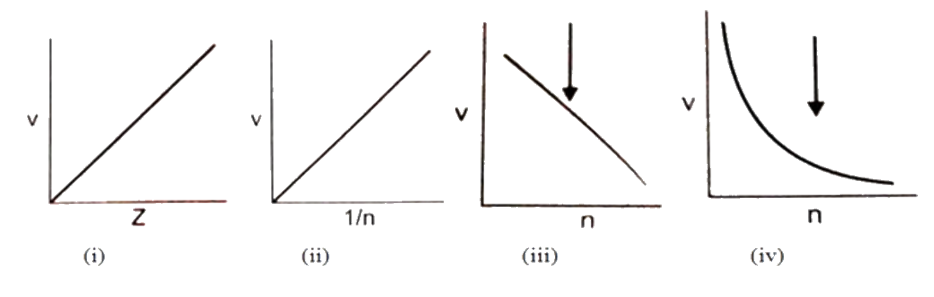
Select the incorrect graph for velocity of e− in an orbit vs. Z, 1n and n :

The correct Answer is:D
To solve the problem of selecting the incorrect graph for the velocity of an electron (e^(-)) in an orbit versus Z, 1/n, and n, we will follow these steps:
Step 1: Understand the relationship between velocity, Z, and n
The velocity (V) of an electron in an orbit is given by the formula:
V=2.18×106Zn
where:
- Z is the atomic number,
- n is the principal quantum number (the orbit number).
Step 2: Analyze the relationship of V with n
From the formula, we can see that:
V∝Zn
This means that the velocity is inversely proportional to n. Therefore, if we plot V against n, we would expect to see a hyperbolic relationship.
Step 3: Analyze the relationship of V with 1/n
Since V is inversely proportional to n, it is directly proportional to 1/n:
V∝1n
If we plot V against 1/n, we would expect to see a linear relationship (straight line).
Step 4: Analyze the relationship of V with Z
Since V is directly proportional to Z:
V∝Z
If we plot V against Z, we would also expect to see a linear relationship (straight line).
Step 5: Evaluate the options
Now, let's evaluate the options based on our analysis:
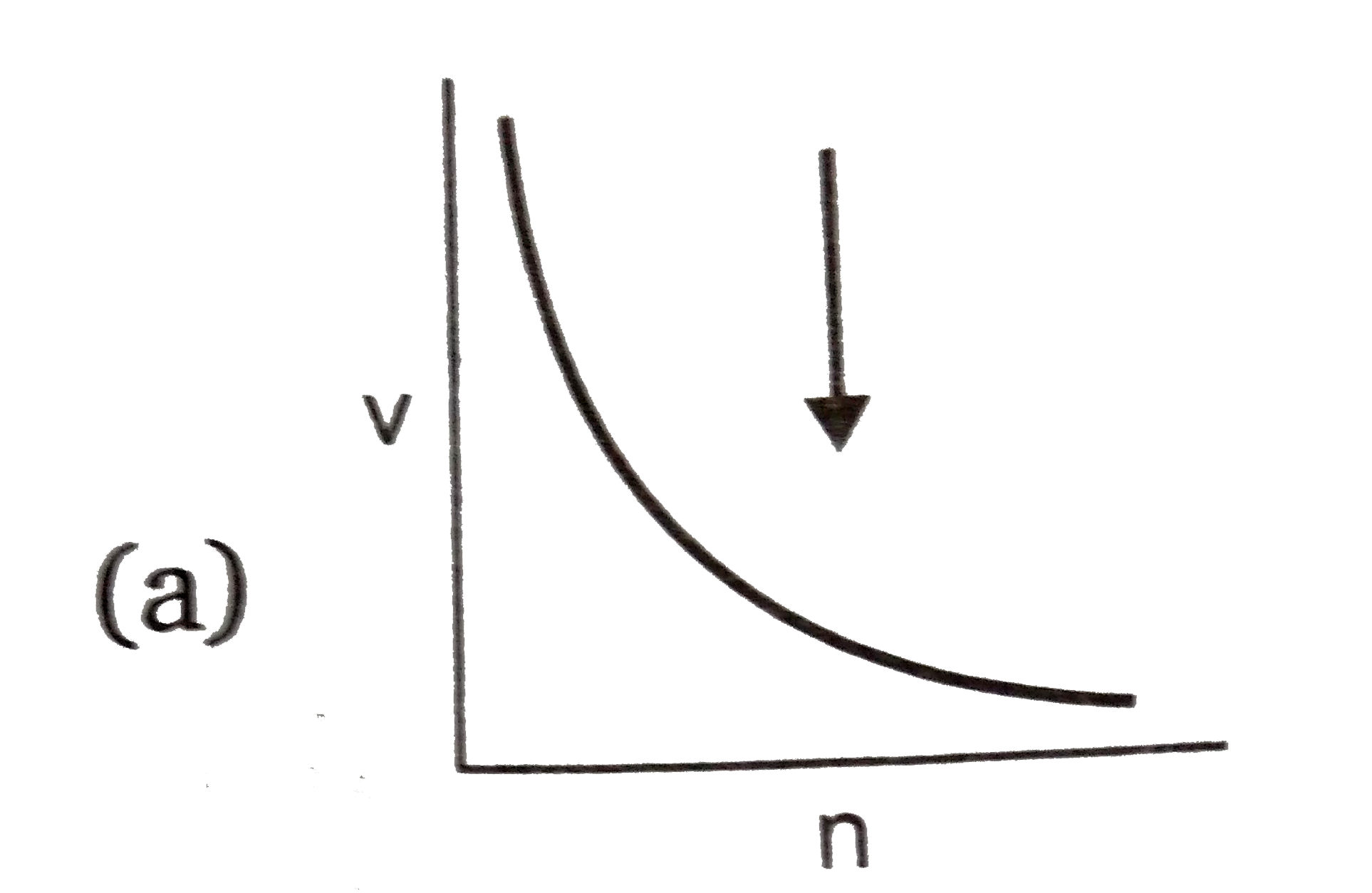
- Option A (V vs n): This should be a hyperbolic graph. (Correct)
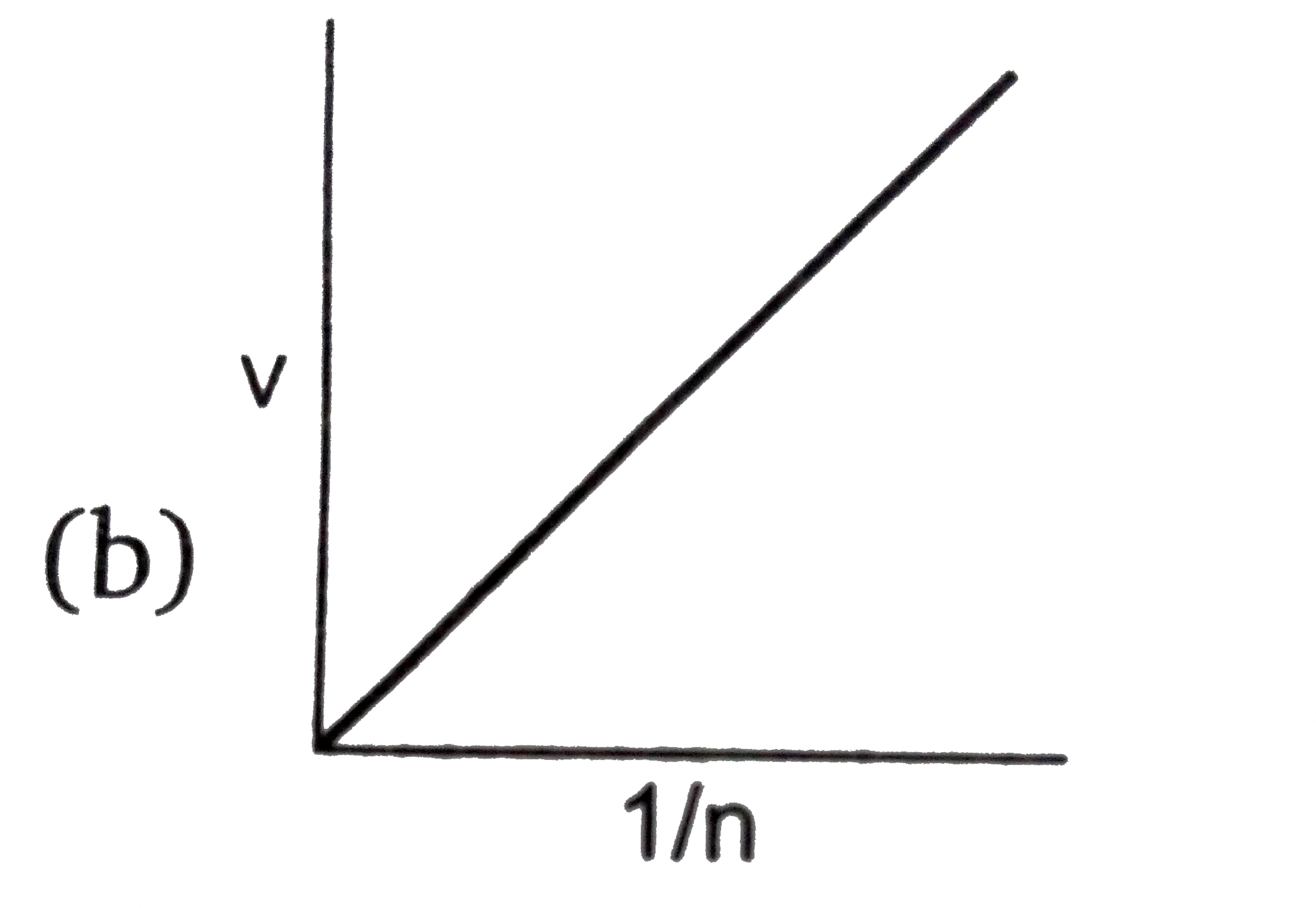
- Option B (V vs 1/n): This should be a straight line. (Correct)
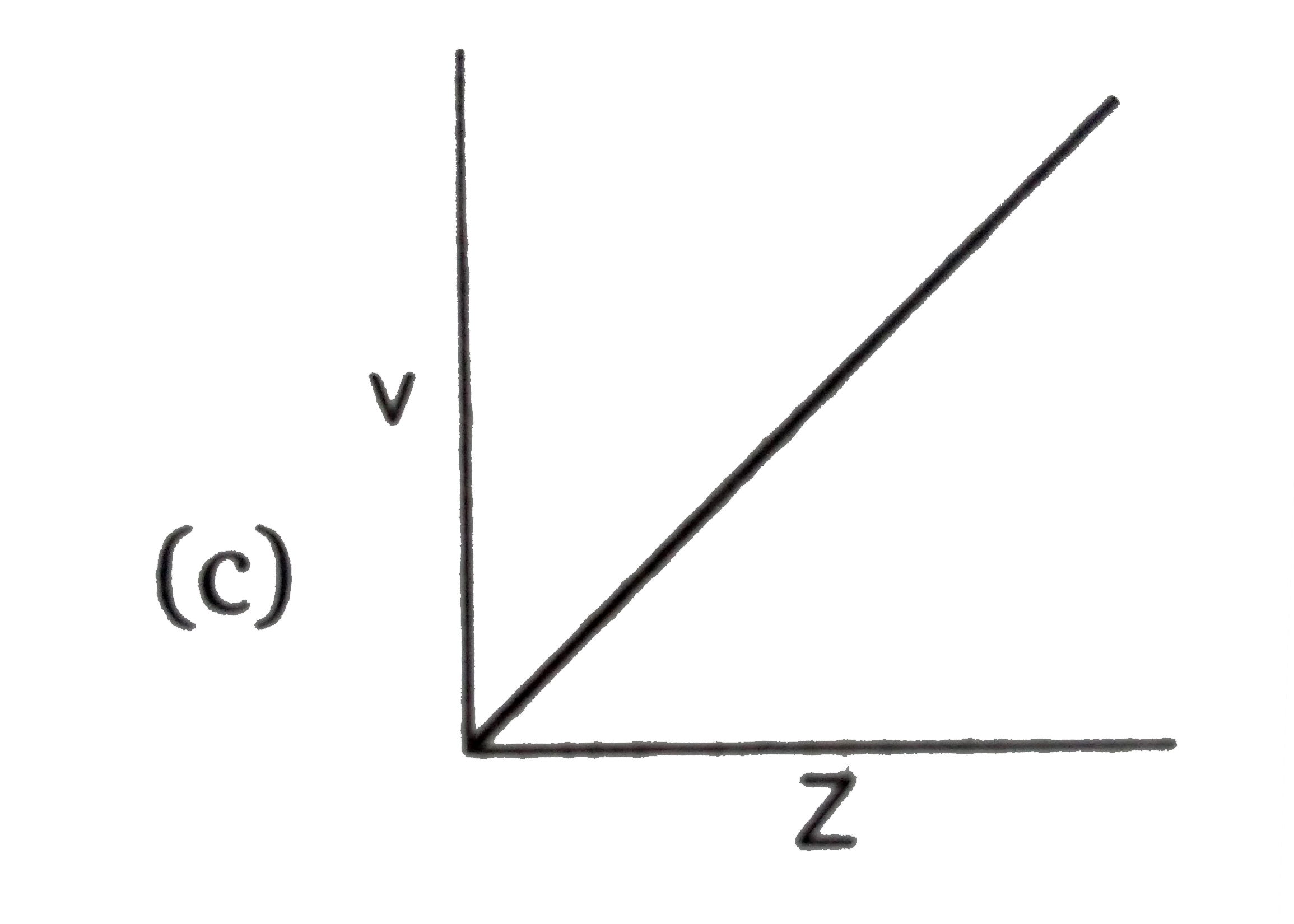
- Option C (V vs Z): This should also be a straight line. (Correct)
- Option D (V vs n): This is incorrectly stated as a straight line, but it should be a hyperbolic graph. (Incorrect)
Conclusion
The incorrect statement is found in Option D, where it incorrectly states that the graph of V against n is a straight line, when it should actually be a hyperbola.
The velocity (V) of an electron in an orbit is given by the formula:
V=2.18×106Zn
where:
- Z is the atomic number,
- n is the principal quantum number (the orbit number).
From the formula, we can see that:
V∝Zn
This means that the velocity is inversely proportional to n. Therefore, if we plot V against n, we would expect to see a hyperbolic relationship.
Since V is inversely proportional to n, it is directly proportional to 1/n:
V∝1n
If we plot V against 1/n, we would expect to see a linear relationship (straight line).
Since V is directly proportional to Z:
V∝Z
If we plot V against Z, we would also expect to see a linear relationship (straight line).
Now, let's evaluate the options based on our analysis:
- Option A (V vs n): This should be a hyperbolic graph. (Correct)
- Option B (V vs 1/n): This should be a straight line. (Correct)
- Option C (V vs Z): This should also be a straight line. (Correct)
- Option D (V vs n): This is incorrectly stated as a straight line, but it should be a hyperbolic graph. (Incorrect)
The incorrect statement is found in Option D, where it incorrectly states that the graph of V against n is a straight line, when it should actually be a hyperbola.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Select the incorrect statements about the plots of ln K vs 1/T
ALinear with slope equal to ΔG∘R and intercept ΔHBCurveCLinear with slope −ΔH∘R and intercept ΔS∘RDnone of theseWhich of the following option(s) is/are independent of both n and Z for H−like species?
Un= Potential energy of electron in nth orbit
KEn= Kinetic energy of electron in nth orbit
ln= Angular momentam of electoron in nth orbit
vn= Velcity of electron in nth orbit
fn= Frequency of electron in nth orbit
Tn= Time period of revolution of electron in nth orbitArnUnBrn×KEn×lnCUn×TnlnDln×fnv2n
If an electron is moving in the nth orbit of the hydrogen atom, then its velocity (vn) for the nth orbit is given as :
View SolutionBohr's model enables us to derive the energy of an electron revolving in nth orbit. For H-atom and hydrogen like species :
En=2π2me4Z2n2h2
or =−13.6Z2n2eVatom−1=21.8×10−19Z2n2Jatom−1
This helps to calculate the radius of an orbit,
rn=0.529n2ZÅ
Bohr's model also explains the occurrence of different spectral lines. The wavelengths of difference line can be given as :
1λ=¯v(incm−1)=R(1n21−1n22)
R=109678cm−1andn2>n1.
What is the ratio of radius of 4th orbit of hydrogen and 3rd orbit of Li2+ ion ?
View SolutionIf the velocity of the revolving electron of He+ in the first orbit (n= 1) is v. the velocity of the electron in the second orbit is:
View SolutionBohr's model enables us to derive the energy of an electron revolving in nth orbit. For H-atom and hydrogen like species :
En=2π2me4Z2n2h2
or =−13.6Z2n2eVatom−1=21.8×10−19Z2n2Jatom−1
This helps to calculate the radius of an orbit,
rn=0.529n2ZÅ
Bohr's model also explains the occurrence of different spectral lines. The wavelengths of difference line can be given as :
1λ=¯v(incm−1)=R(1n21−1n22)
R=109678cm−1andn2>n1.
Which transition between Bohr's orbits corresponds to third line in Lyman series?
View SolutionAn electron in a hydrogen atom is considered to be revolving around a proton with a velocity e2n in a circular orbit of radius n2me2. If I is the equivalent current, express it in terms of m, e, n.
View SolutionBohr's model enables us to derive the energy of an electron revolving in nth orbit. For H-atom and hydrogen like species :
En=2π2me4Z2n2h2
or =−13.6Z2n2eVatom−1=21.8×10−19Z2n2Jatom−1
This helps to calculate the radius of an orbit,
rn=0.529n2ZÅ
Bohr's model also explains the occurrence of different spectral lines. The wavelengths of difference line can be given as :
1λ=¯v(incm−1)=R(1n21−1n22)
R=109678cm−1andn2>n1.
What is the experimental evidence in support of the fact that electronic energies in an atom are quantized ?
View Solution