Select the incorrect graph for velocity of e− in an orbit vs. Z, 1n and n :

The correct Answer is:D
To solve the problem of selecting the incorrect graph for the velocity of an electron in an orbit versus Z, 1n, and n, we can follow these steps:
1. Understand the relationship between velocity, Z, and n:
The velocity v of an electron in an orbit is derived from the balance of forces acting on it. The centrifugal force is equal to the electrostatic force. This can be expressed as:
mv2/r=kZe24πϵ0r2
where m is the mass of the electron, v is its velocity, r is the radius of the orbit, Z is the atomic number, e is the charge of the electron, and k is Coulomb's constant.
2. Use angular momentum quantization:
The angular momentum of the electron is quantized:
mvr=nh2π
where n is a principal quantum number and h is Planck's constant.
3. Derive the formula for velocity:
By substituting r from the angular momentum equation into the force balance equation, we can derive that:
v=2π2ke2Znh
This shows that the velocity v is proportional to Zn:
v∝Zn
4. Analyze the graphs:
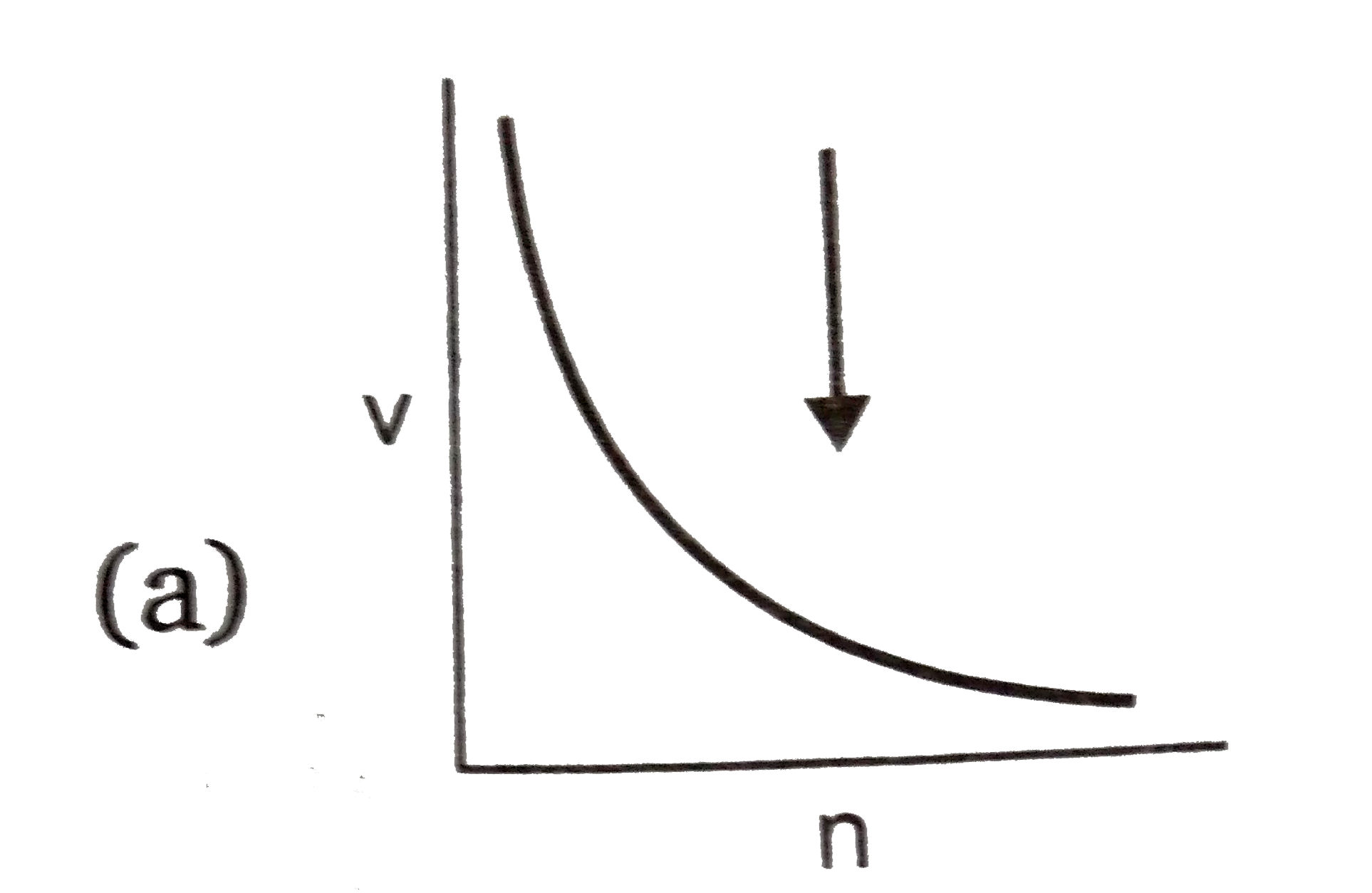
- Graph A (v vs n): Since v is inversely proportional to n, this graph should be a rectangular hyperbola. This is correct.
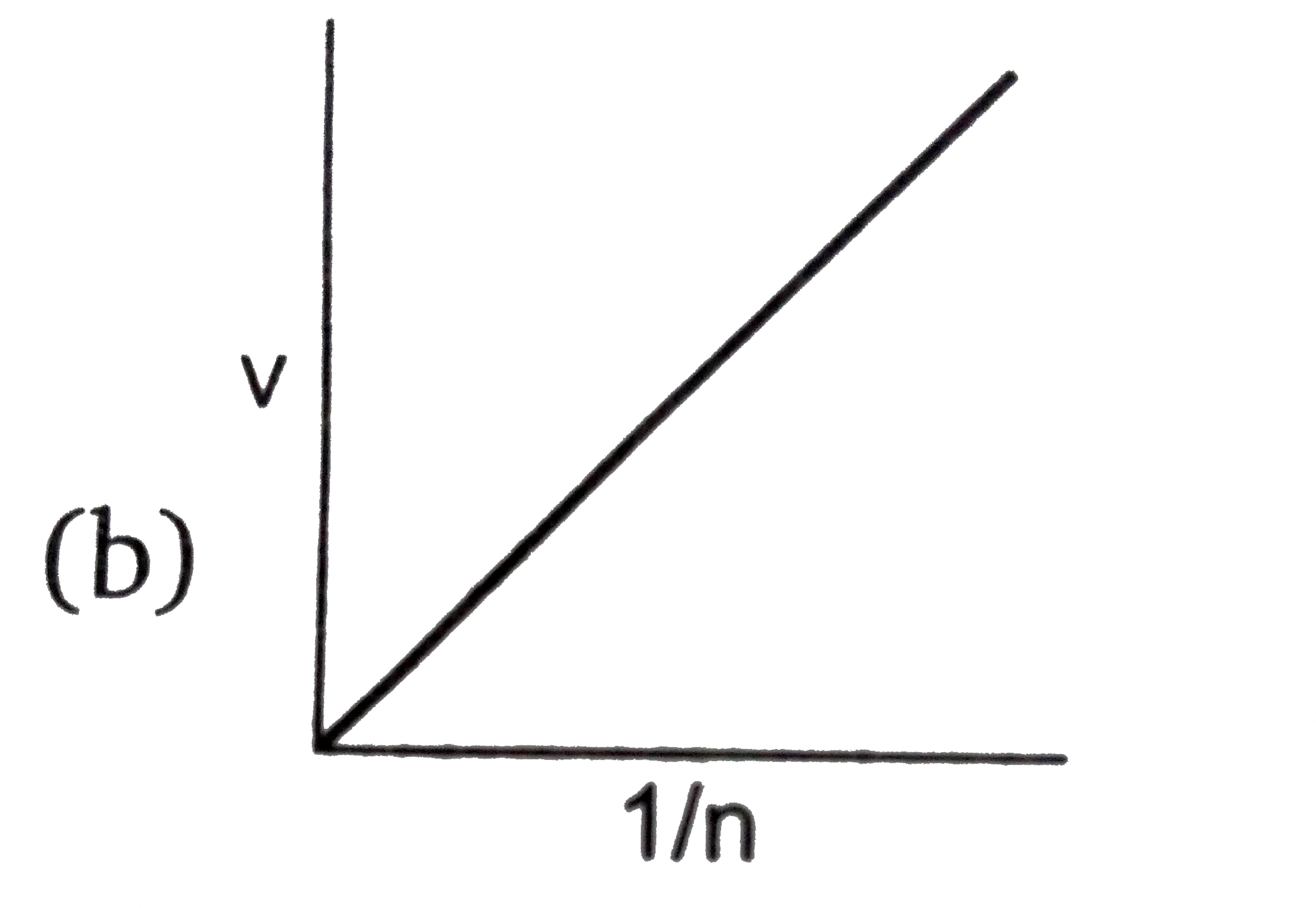
- Graph B (v vs 1n): Since v is directly proportional to 1n, this graph should be a straight line passing through the origin. This is correct.
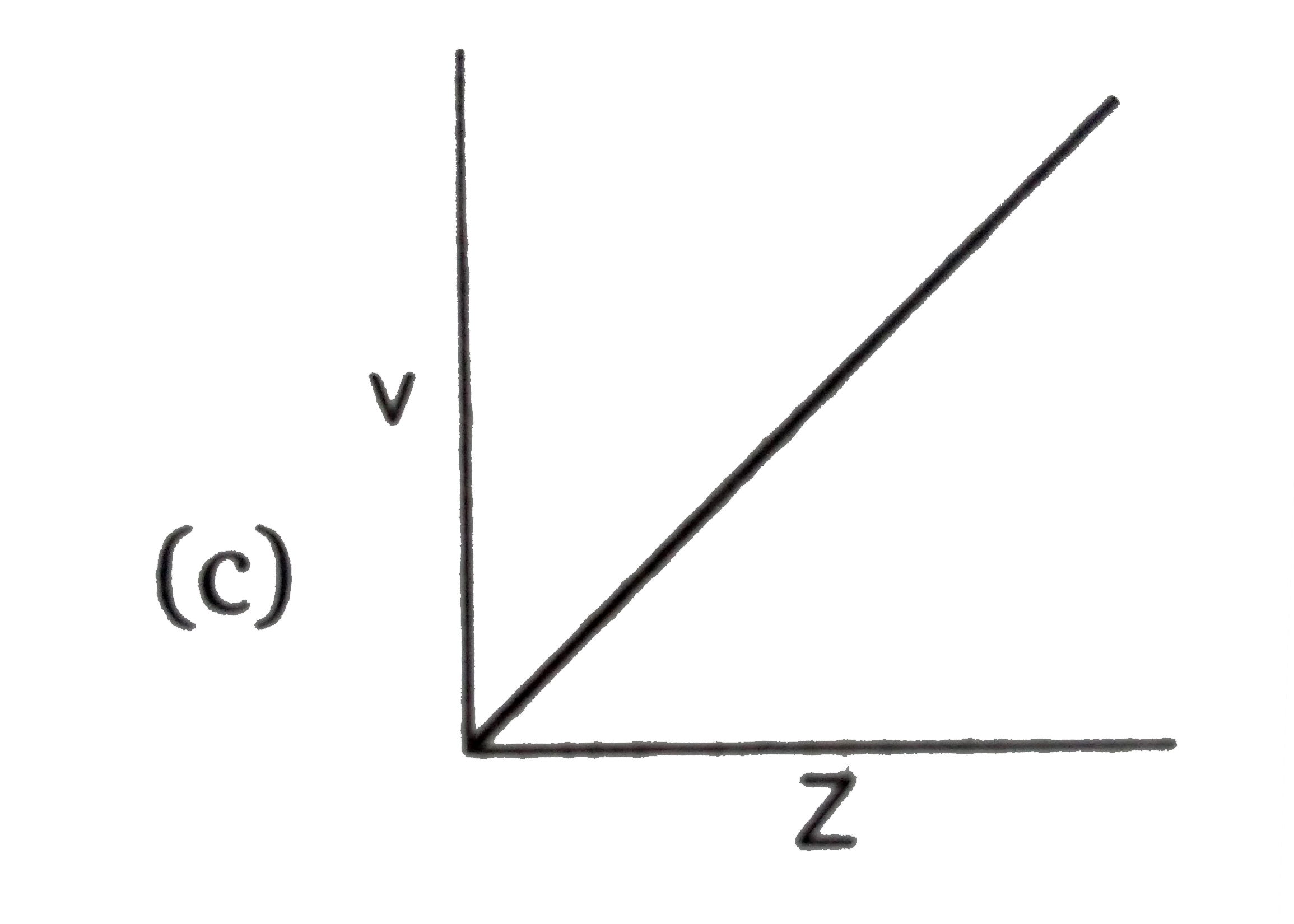
- Graph C (v vs Z): Since v is directly proportional to Z, this graph should also be a straight line passing through the origin. This is correct.
- Graph D (v vs n): This graph is claimed to be a straight line with a negative slope, which contradicts the derived relationship that v is inversely proportional to n (should be a rectangular hyperbola). This is incorrect.
5. Conclusion:
The incorrect graph is Graph D, which incorrectly represents the relationship between velocity and n.
Final Answer:
The incorrect graph is D.
The velocity v of an electron in an orbit is derived from the balance of forces acting on it. The centrifugal force is equal to the electrostatic force. This can be expressed as:
mv2/r=kZe24πϵ0r2
where m is the mass of the electron, v is its velocity, r is the radius of the orbit, Z is the atomic number, e is the charge of the electron, and k is Coulomb's constant.
The angular momentum of the electron is quantized:
mvr=nh2π
where n is a principal quantum number and h is Planck's constant.
By substituting r from the angular momentum equation into the force balance equation, we can derive that:
v=2π2ke2Znh
This shows that the velocity v is proportional to Zn:
v∝Zn
- Graph A (v vs n): Since v is inversely proportional to n, this graph should be a rectangular hyperbola. This is correct.
- Graph B (v vs 1n): Since v is directly proportional to 1n, this graph should be a straight line passing through the origin. This is correct.
- Graph C (v vs Z): Since v is directly proportional to Z, this graph should also be a straight line passing through the origin. This is correct.
- Graph D (v vs n): This graph is claimed to be a straight line with a negative slope, which contradicts the derived relationship that v is inversely proportional to n (should be a rectangular hyperbola). This is incorrect.
The incorrect graph is Graph D, which incorrectly represents the relationship between velocity and n.
The incorrect graph is D.
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
Which of the following option(s) is/are independent of both n and Z for H−like species?
Un= Potential energy of electron in nth orbit
KEn= Kinetic energy of electron in nth orbit
ln= Angular momentam of electoron in nth orbit
vn= Velcity of electron in nth orbit
fn= Frequency of electron in nth orbit
Tn= Time period of revolution of electron in nth orbit
View SolutionIf, in a hydrogen atom, radius of nth Bohr orbit is rn frequency of revolution of electron in nth orbit is fn and area enclosed by the nth orbit is An , then which of the pollowing graphs are correct?
View SolutionCalculate the velocity of the electron in the third orbit of hydrogen atom
Hint :v=2.18×106znm/s
View SolutionShow the nature of the following graph for a satellite orbiting the earth.
(a) KE vs orbitial radius R (b) PE vs orbital radius r (c ) TE vs orbital radius R.
View SolutionCalculate the energy associated with the first orbit of He+.What is the radius of this orbit ?
Hint :En=−2.18×10−18(Z2n2)J/atom
He+(Z=2)
rn=52.9(n2)Z pm
View Solutionn, l and m values of the 2pz orbital are
View SolutionIf the magnitude of energy of the electron in nth Bohr orbit is EnandJn is its angular momentum , then
View SolutionIn the Bohr's model , for unielectronic species following symbols are used
rn,z→ Radius of nth orbit with atomic number "z"
Un,z→ Potential energy of electron in nth orbit with atomic number "z"
Kn,z→ Kinetic energy of electron in nth orbit with atomic number "z"
Vn,z→ Velocity of electon in nth orbit with atomic number "z"
Tn,z→ Time period of revolution of electon in nth orbit with atomic number "z"
Calculate z in all in cases.
(i)U1,2:K1,z=−8:9
(ii)r1,z:r2,1=1:12
(iii)v1,z:v3,1=15:1
(iv)T1,2:T2,z=9:32
Report your answer as (2r-p-q-s) where p,q,r and s represents the value of "z" in parts (i),(ii),(iii),(iv).
View SolutionIn hydrogen atom, if the difference in the energy of the electron in n=2 and n=3 orbits is E, the ionization energy of hydrogen atom is
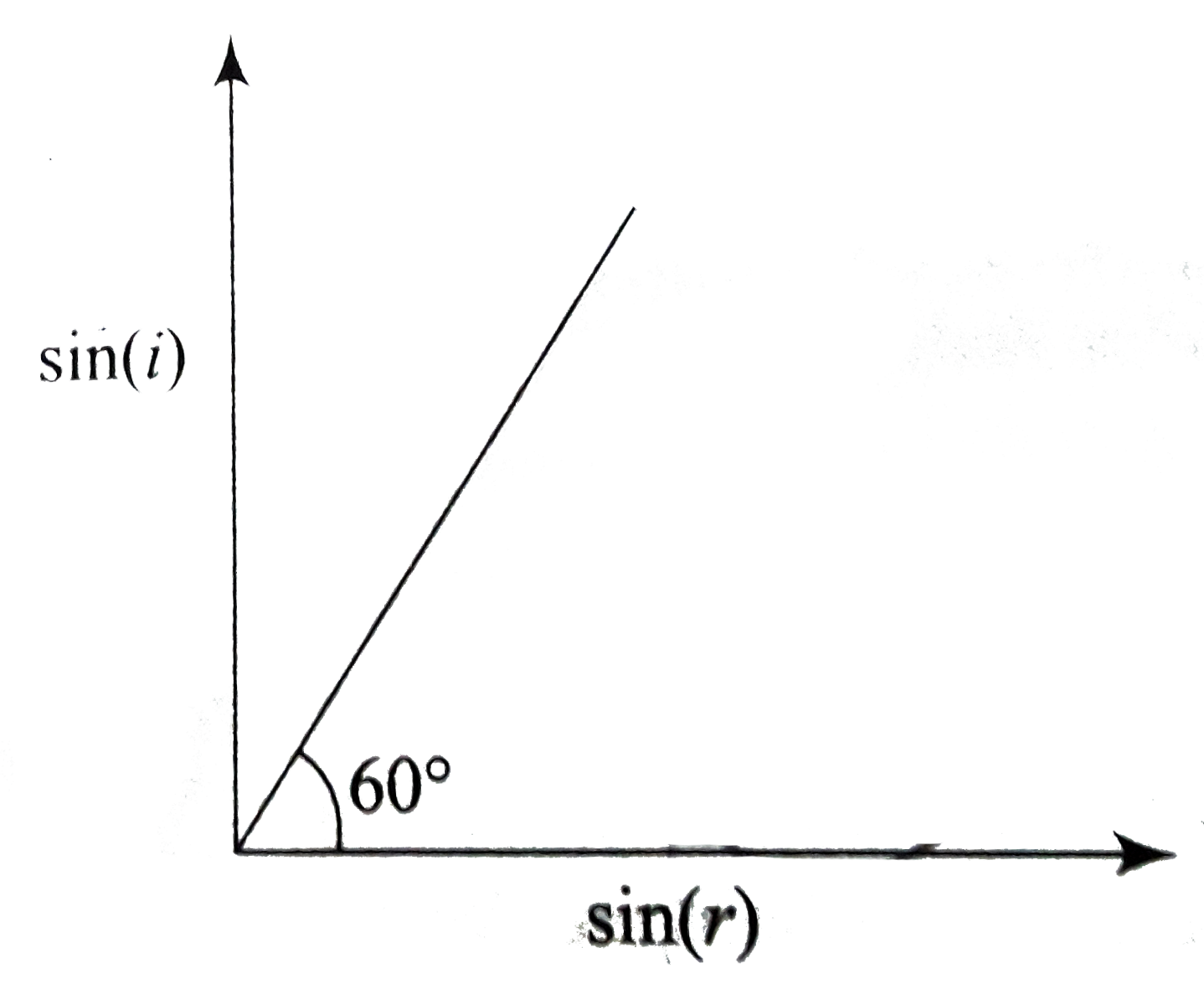
View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
View Solution
