The average velocity of CO2 at the temperature T1K and maximum (most) proable velocity of CO2 at the temperature T2K is 9×104cms−1. Calculate the values of T1 and T2.
To solve the problem, we need to calculate the temperatures T1 and T2 using the given velocities of carbon dioxide (CO2) at those temperatures.
1. Identify the Given Information:
- Average velocity of CO2 at temperature T1 is 9×104cm/s.
- Most probable velocity of CO2 at temperature T2 is also 9×104cm/s.
- Convert the velocity to SI units:
9×104cm/s=9×102m/s
2. Use the Formula for Average Velocity:
- The average velocity uaverage is given by:
uaverage=√8RTπM
- Set this equal to the average velocity at T1:
√8RT1πM=9×102
3. Substitute Known Values:
- Use R=8.314J/(mol K) and M=44×10−3kg/mol:
√8×8.314×T1π×44×10−3=9×102
4. Square Both Sides to Eliminate the Square Root:
8×8.314×T1π×44×10−3=(9×102)2
5. Calculate the Right Side:
(9×102)2=81×104=8.1×105
6. Rearranging the Equation:
T1=8.1×105×π×44×10−38×8.314
7. Perform the Calculation:
- Calculate T1:
T1=8.1×105×3.14×44×10−38×8.314
- After performing the calculations, we find:
T1≈1682.5K
8. Use the Formula for Most Probable Velocity:
- The most probable velocity umost probable is given by:
umost probable=√2RTM
- Set this equal to the most probable velocity at T2:
√2RT2M=9×102
9. Substitute Known Values:
√2×8.314×T244×10−3=9×102
10. Square Both Sides:
2×8.314×T244×10−3=(9×102)2
11. Rearranging the Equation:
T2=8.1×105×44×10−32×8.314
12. Perform the Calculation:
- Calculate T2:
T2=8.1×105×44×10−32×8.314
- After performing the calculations, we find:
T2≈2143.4K
Final Answers:
- T1≈1682.5K
- T2≈2143.4K
- Average velocity of CO2 at temperature T1 is 9×104cm/s.
- Most probable velocity of CO2 at temperature T2 is also 9×104cm/s.
- Convert the velocity to SI units:
9×104cm/s=9×102m/s
- The average velocity uaverage is given by:
uaverage=√8RTπM
- Set this equal to the average velocity at T1:
√8RT1πM=9×102
- Use R=8.314J/(mol K) and M=44×10−3kg/mol:
√8×8.314×T1π×44×10−3=9×102
8×8.314×T1π×44×10−3=(9×102)2
(9×102)2=81×104=8.1×105
T1=8.1×105×π×44×10−38×8.314
- Calculate T1:
T1=8.1×105×3.14×44×10−38×8.314
- After performing the calculations, we find:
T1≈1682.5K
- The most probable velocity umost probable is given by:
umost probable=√2RTM
- Set this equal to the most probable velocity at T2:
√2RT2M=9×102
√2×8.314×T244×10−3=9×102
2×8.314×T244×10−3=(9×102)2
T2=8.1×105×44×10−32×8.314
- Calculate T2:
T2=8.1×105×44×10−32×8.314
- After performing the calculations, we find:
T2≈2143.4K
- T1≈1682.5K
- T2≈2143.4K
Topper's Solved these Questions
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Fill In The Blanks)
25 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Ture False)
25 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Concept Application 5.3
1 Videos
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective
11 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
The average velocity of CO2 at T K is 9×104cms−1. The value of T is
View Solution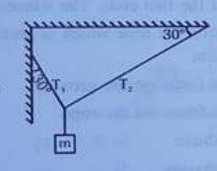
Calculate T1&T2.
View Solution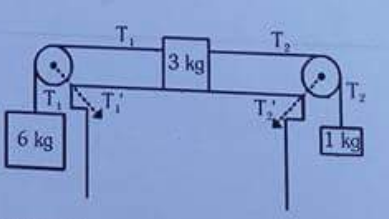
Calculate a, T1,T2,T1'&T2'.
View SolutionThe graph between the (velocity2) and temperature T of a gas is
View SolutionCalculate the average velocity of CO2 molecule at S.T.P.
View SolutionThe average speed at temperature T∘C of CH4(g) is √2888×103ms−1. What is the value of T ?
View SolutionThe rms velocity of CO2 at temperature T(in Kelvin) is x cm s−1. At what temperature (in Kelvin) would the rms velocity of nitrous oxide be 4xcms−1?
View SolutionAt what temperature will the rms velocity of CO2 be same as the average velocity of SO2 at 500K?
View SolutionCalculate the temperature of which CO2 has the same RMS velocity as that of O2 at S.T.P
View SolutionCO2 at 600 bar and a temperature above Tc(Tc=304.15K) is called
View Solution
