The density of ice is 0.921 g cm−3. Calculate the mass of a cubic block of ice which is 76 mm on each side.
The correct Answer is:A, B, D
To calculate the mass of a cubic block of ice with a given density, we can follow these steps:
Step 1: Understand the given data
- Density of ice = 0.921 g/cm³
- Each side of the cube = 76 mm
Step 2: Convert the side length from mm to cm
To convert millimeters to centimeters, we divide by 10:
Side length in cm=76 mm10=7.6 cm
Step 3: Calculate the volume of the cube
The volume V of a cube is given by the formula:
V=side3
Substituting the side length:
V=(7.6 cm)3=7.6×7.6×7.6=438.976 cm3
We can round this to:
V≈439 cm3
Step 4: Use the density to find the mass
The mass m can be calculated using the formula:
m=density×volume
Substituting the values:
m=0.921 g/cm3×439 cm3
Calculating the mass:
m≈404.199 g
We can round this to:
m≈404.2 g
Final Answer
The mass of the cubic block of ice is approximately 404.2 grams.
---
- Density of ice = 0.921 g/cm³
- Each side of the cube = 76 mm
To convert millimeters to centimeters, we divide by 10:
Side length in cm=76 mm10=7.6 cm
The volume V of a cube is given by the formula:
V=side3
Substituting the side length:
V=(7.6 cm)3=7.6×7.6×7.6=438.976 cm3
We can round this to:
V≈439 cm3
The mass m can be calculated using the formula:
m=density×volume
Substituting the values:
m=0.921 g/cm3×439 cm3
Calculating the mass:
m≈404.199 g
We can round this to:
m≈404.2 g
The mass of the cubic block of ice is approximately 404.2 grams.
Topper's Solved these Questions
- SOME BASIC CONCEPTS OF CHEMISTRY Book:MODERN PUBLICATIONChapter:SOME BASIC CONCEPTS OF CHEMISTRY Exercise:CONCEPTUAL QUESTION 1
Explore 12 Videos
- SOME BASIC CONCEPTS OF CHEMISTRY Book:MODERN PUBLICATIONChapter:SOME BASIC CONCEPTS OF CHEMISTRY Exercise:CONCEPTUAL QUESTION 2
Explore 14 Videos
- SOME BASIC CONCEPTS OF CHEMISTRY Book:MODERN PUBLICATIONChapter:SOME BASIC CONCEPTS OF CHEMISTRY Exercise:COMPETITION FILE (INTEGER TYPE AND NUMERICAL VALUE TYPE QUESTIONS)
Explore 10 Videos
- S-BLOCK ELEMENTS ( ALKALI AND ALKALINE EARTH METALS ) Book:MODERN PUBLICATIONChapter:S-BLOCK ELEMENTS ( ALKALI AND ALKALINE EARTH METALS ) Exercise:UNIT PRACTICE TEST
Explore 13 Videos
- STATES OF MATTER : GASES AND LIQUIDSBook:MODERN PUBLICATIONChapter:STATES OF MATTER : GASES AND LIQUIDSExercise:UNIT PRACTICE TEST
Explore 13 Videos
Similar Questions
Gaseous ozone is bubbled through water-ice mixture at 0∘C. As the O3(g) decomposes to form O2(g), the enthalpy of reaction is absorbed by the resulting ice. Given that the heat of fusion of ice is 6.0095 kJmol−1 , calculate the mass of ice that melts for each gram of O3 that decomposes.
2O3(g)→3O2(g),ΔH=−285.kJ
View SolutionThe density of ice is 0.918gcm−3 and that of water is 1.03gcm−3. An iceberg floats with a portion of 224m3 outside the surface of water. Find the total volume of the iceberg.
View Solution
Knowledge Check
A cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is
 A200PaB620PaC900PaD800Pa
A200PaB620PaC900PaD800PaThe density of ice is 0.92 g/cm3 and the density of seawater is 1.03 g/cm3. A large iceberg floats in Arctic waters. What fraction of the volume of the iceberg is exposed?
A0.080 %B11 %C0.89D0.92The density of ice xcm−3 and that of water is ygcm−3. What is the change in volume when mg of ice melts?
Am(y−x)cm3By−xmcm3Cmxy(x−y)cm3Dm((1y−1x)cm3.
Calculate the mass of a body whose volume is 2m3 and density 0.52gcm3.
View SolutionA hollow sphere of glass whose external and internal radii are 11cm and 9cm respec-tively is completely filled with ice at 0∘C and placed in a both of boiling water How long will it take for the ice to melt completely ? Givne that density of ice =0.9g/cm3 latent heat of fusion of ice =80cal/g and thermal conductivity of glass =0.002cal/cm−s∘C .
View SolutionAn ice layer of thickness 3 cm is formed on a lake. How much time will it take to increase the thickness of ice by 2 mm if temperature of air is −30∘C ? Take, Density of ice =1gcm−3 , Latent heat of ice =80calg−1 , Conductivity of ice =0.008cals−1cm−1∘C−1
View SolutionA hollow sphere of glas whose external and internal radii are 11 cm and 9 cm respectively is completely filled with ice at 0∘C and placed in a bath of boiling water. How long will it take for the ice to melt completely? Given that density of ice = 0.9g/cm3, latent heat of fusion of ice =80cal/g and thermal conductivity of glass =0.002cal/cm−s∘C.
View SolutionA cubical block of wood 10cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6gcm−3 and density of water is 1gcm−3. The mass of the block is
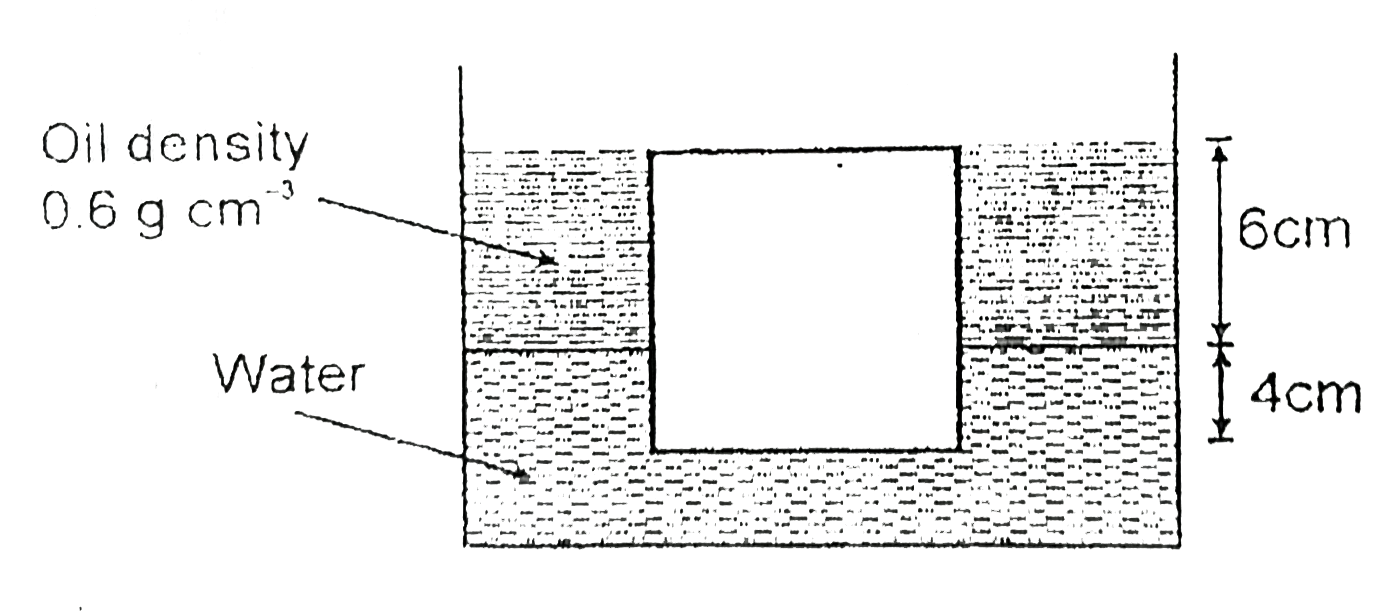
View Solution