The empty space left between the spheres in close-packed structure is called voids. The decreasing order of the size of voids is
cubic > octahedral > tetrahedral > trigonal
octahedral > tetrahedral > trigonal > cubic
tetrahedral > trigonal > cubic > octahedral
trigonal > cubic > octahedral > tetrahedral
The correct Answer is:A
To determine the decreasing order of the size of voids in a close-packed structure, we need to analyze the types of voids present and their respective sizes. The voids are categorized as follows:
1. Cubic Voids: These are the largest voids formed in a close-packed structure. In a cubic void, there are a total of 8 lattice points surrounding it. This makes it the largest type of void.
2. Octahedral Voids: These are the second largest voids. An octahedral void is surrounded by 6 lattice points. This makes it smaller than the cubic void but larger than the tetrahedral void.
3. Tetrahedral Voids: These voids are smaller than octahedral voids. A tetrahedral void is surrounded by 4 lattice points, making it smaller than the octahedral void.
4. Trigonal Voids: These are the smallest voids in a close-packed structure. A trigonal void is surrounded by 3 lattice points, making it the smallest type of void.
Now, we can summarize the sizes of the voids in decreasing order:
- Cubic Voids (largest)
- Octahedral Voids
- Tetrahedral Voids
- Trigonal Voids (smallest)
Thus, the decreasing order of the size of voids is:
Cubic > Octahedral > Tetrahedral > Trigonal
- Octahedral Voids
- Tetrahedral Voids
- Trigonal Voids (smallest)
Topper's Solved these Questions
Similar Questions
Show that in a cubic close packed structure, eight tetrahedral voids are present per unit cell.
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound isView Solution
Knowledge Check
- Question 1 - Select One
The decreasing order of the size of void is ______.
ACubic gt Octahedral gt Tetrahedral gt TrigonalBTrigonal gt Tetrahedral gt Octahedral gt cubicCTrigonal gtOctahedral gt Trtrahedral gt cubicDCubic gt tetrahedral gt Octahedral gt trigonal - Question 2 - Select One
The decreasing order of the size of void is ______.
Acubic gt octahedral gt tetrahedral gt trigonalBtrigonal gt tetrahedral gt octahedral gt cubicCtrigonal gt octahedral gt tetrahedral gt cubicDcubic gt tetrahedral gt octahedral gt trigonal - Question 3 - Select One
The empty space in the hexogonal close packing is……..% while that in the body-centred cubic packing is ………%
A26%B32%C34%D38%
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
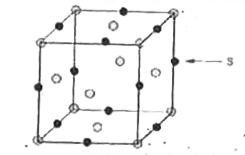 View Solution
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defectView SolutionThe percent of empty space in a unit cell of hexagonal close-packed structure is-
View SolutionIn a hexagonal close packed (hcp) structure of spheres, the fraction of the volume occupied by the sphere is A. In a cubic close packed structure, the fraction is B. The relation between A and B is
View Solution

