The number of geometric isomers that can exist for square planar $[P t (C 1) (p y) (N H_{3}) {(N H_{2} O H)}_{2}^{+}]$ is (py = pyridine).

A

2

B

3

C

4

D

6

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The complex is of the type [Mabcd] M
M $=$ metal
a,b,c,d $=$ Monodentate ligands.

|

Updated on:21/07/2023

Class 12 CHEMISTRY COORDINATION COMPOUNDS

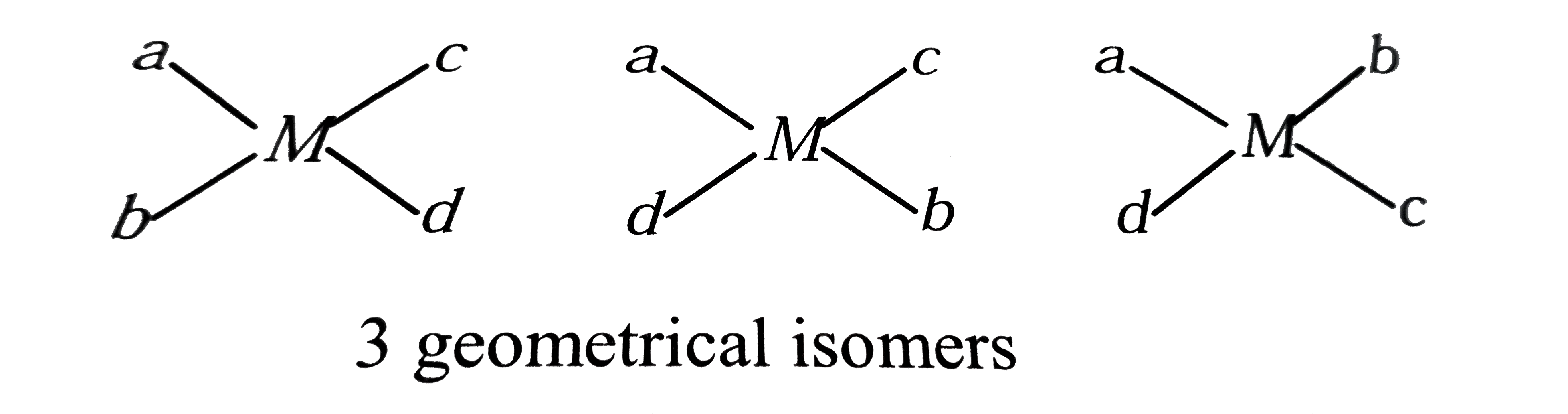
Topper's Solved these Questions

BOOK - ERRORLESS CHAPTER - COORDINATION CHEMISTRYEXERCISE - JEE SECTION MORE THAN ONE CHOICE CORRECT ANSWER
13videos
COORDINATION CHEMISTRY
BOOK - ERRORLESS CHAPTER - COORDINATION CHEMISTRYEXERCISE - JEE SECTION REASONING TYPE QUESTIONS
7videos
COORDINATION CHEMISTRY
BOOK - ERRORLESS CHAPTER - COORDINATION CHEMISTRYEXERCISE - CRITICAL THINKING OBJECTIVE QUESTIONS
18videos
COORDINATION CHEMISTRY
BOOK - ERRORLESS CHAPTER - CLASSIFICATION OF ELEMENTS AND PERIODIC PROPERTIES EXERCISE - JEE Section Matrix Match type questions
2videos
CLASSIFICATION OF ELEMENTS AND PERIODIC PROPERTIES
BOOK - ERRORLESS CHAPTER - D & P-BLOCK ELEMENTSEXERCISE - JEE Section (Numeric answer type questions)
2videos
D & P-BLOCK ELEMENTS

Similar Questions

Knowledge Check

Question 1 - Select One
The number of geometric isomers that can exist for square planar $[P t (C 1) (p y) (N H_{3}) {(N H_{2} O H)}_{2}^{+}]$ is (py = pyridine).
A4
B6
C2
D3
Question 2 - Select One
The number of geometric isomers that can exist for square planar ${[P t (C l) (p y) (N H_{3}) (N H_{2} O H)]}^{+}$ is (py=pyridine)
A2
B3
C4
D6
Question 3 - Select One
The number of geometric isomers that can exist for square planner complex ion ${[P t (C I) (P Y) (N H_{3}) (N H_{2} O H)]}^{+}$ is (Py = pyridine) :
A4
B6
C2
D3

ERRORLESS -COORDINATION CHEMISTRY-JEE SECTION Only one choice answer

Home
Ask Doubt
Profile