The spein multipltcity for the orbital enryron si 2s+1where (s) is total enrctrons pin. The spin multiplicity for stage (I) , (II) and (III)are respectively
.
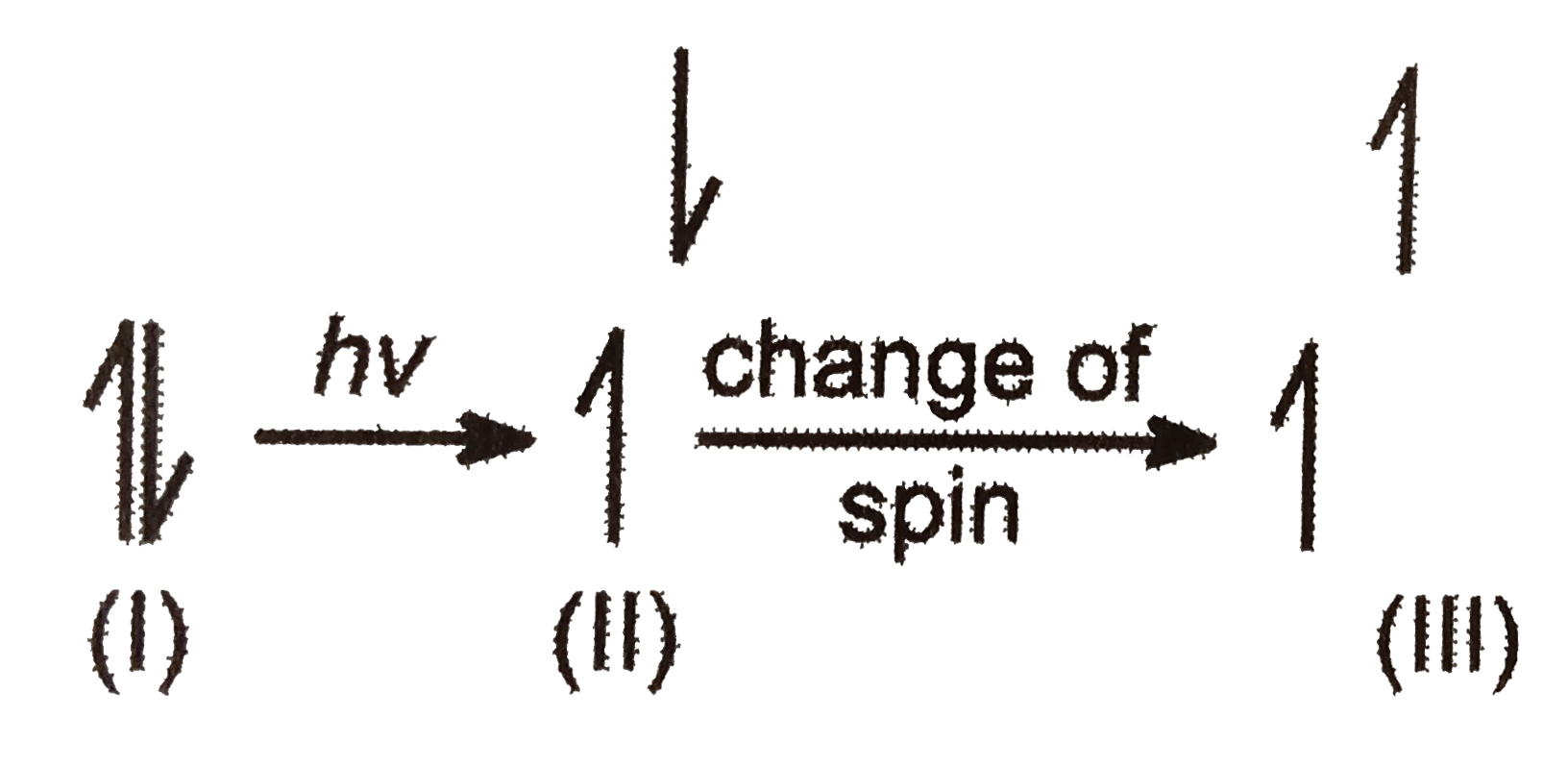1,1,1
1,2,3
1,13
1,3,1
The correct Answer is:C
For (I) (Ground state )
Total sjpins s=+12−12=0
∴ Spin multiplicity =(2×0)+1=1
For (II) (singlet excited state )
Total spin S=+12=12=1
∴ Spin multiplicity =(2×1)=1=3.
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 3B
19 Videos
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 4
39 Videos
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise
19 Videos
- CHEMICAL BONDINGBOOK - P BAHADURCHAPTER - CHEMICAL BONDINGEXERCISE - Exercise 7
11 Videos
Similar Questions
Two satellites S1 and S2 resolve round a planet in coplaner circular orbit in the same sense. Their period of revolution are 1 hour and 8 hour respectively. The radius of the orbit of S1 is 104km. When S2 is closest to S1, find
(a) The speed of S2 relative to S1,
(b) The angular speed of S2 actually observed by an astronaut is S1
View SolutionThe sum of spins of all the electron is the total spins(S) and (2S+1) is called spin multiplicity of the electronic configuration. Hund's rule defines the ground state configuration of electrons in degenerate orbitals i.e., orbitals within the same sub-shell which have the same values of n and l, states thta in degenerate orbitals pairing of electrons does not occur unless and until all such orbitals are filled singly with their parallel spin. A spinning electron behaves as though it were a tiny bar magnet with poles lying on the axis of spin. The magnetic moment of any atom, ion or molecule due to spin called spin-only magnetic moment (ms) is given by the formula.
μs=√n(n+2)B.M
where n= number of unpaired electron(s)
The spin-only magnetic moment of Cr3+?
View Solution
Knowledge Check
In the figure shows, all the capacitors are initially uncharged.
Case I: only switch S1 is closed
Case II: only switch S2 is closed
Case III: both swithces are closed
Find the ratio of the total energy stored in the system of capacitors for the cases I, II, and III, respectively.
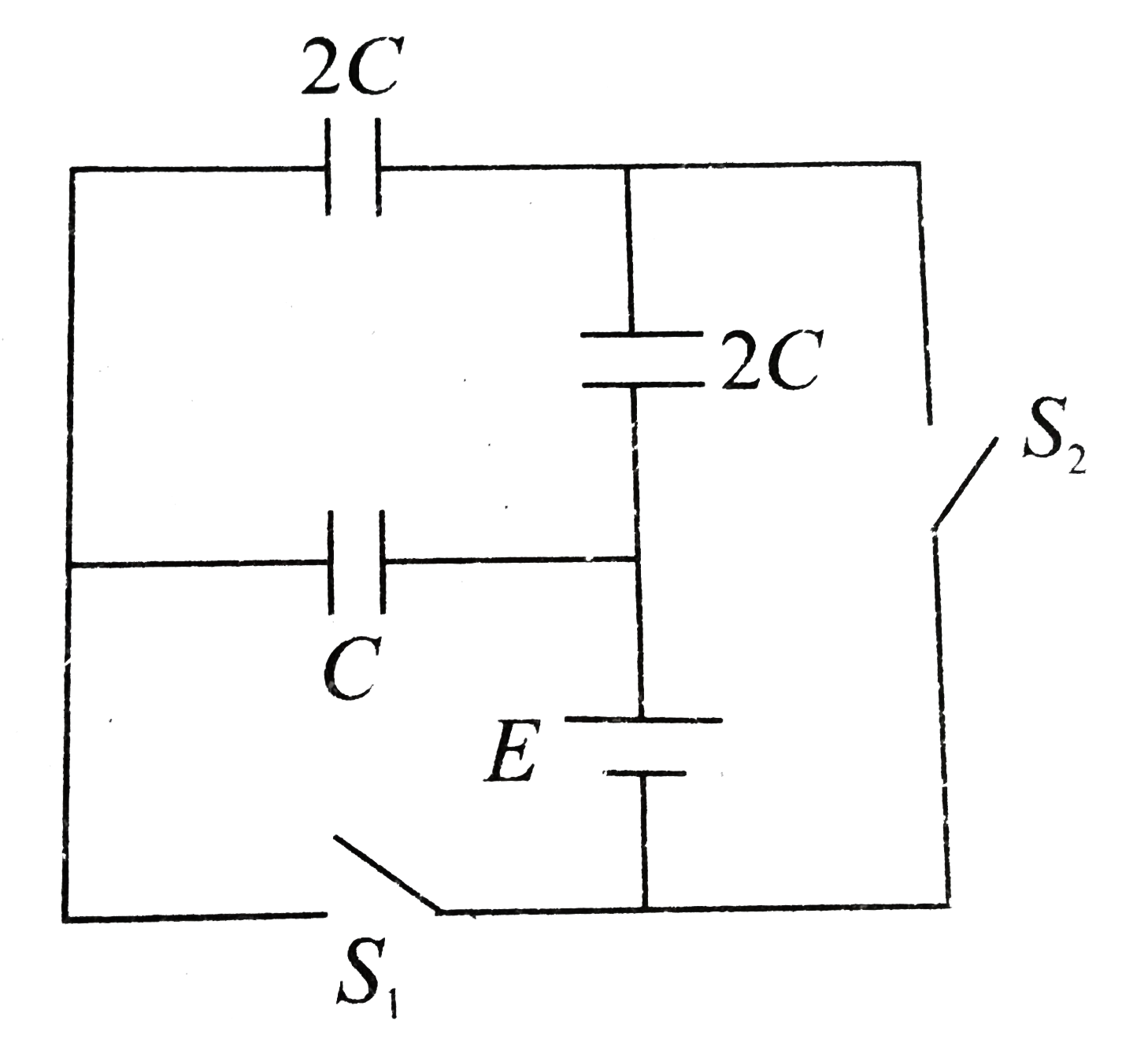A1:2:3B5:7:9C6:8:9D9:7:6The sum of spins of all the electron is the total spins(S) and (2S+1) is called spin multiplicity of the electronic configuration. Hund's rule defines the ground state configuration of electrons in degenerate orbitals i.e., orbitals within the same sub-shell which have the same values of n and l, states thta in degenerate orbitals pairing of electrons does not occur unless and until all such orbitals are filled singly with their parallel spin. A spinning electron behaves as though it were a tiny bar magnet with poles lying on the axis of spin. The magnetic moment of any atom, ion or molecule due to spin called spin-only magnetic moment (ms) is given by the formula.
μs=√n(n+2)B.M
where n= number of unpaired electron(s)
The spin-multiplicity of Fe3+[Ec=[Ar]3d5) in its ground stateA6B2C3D4Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. The orbital angular momentum of a 2p-electron is:A√3hB√6hCzeroD√2h2π
Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. In any subshell, the maximum number of electrons having same value of spin quantum numbers is:
View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. Total spin of Mn2+(Z=25) ion will be:
View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. Which of the following electronic configurations have four spin multiplicity?
View SolutionIt is tempting to think that all possible transition are permissible and that an atomic spectrum arises from the transition of an electron from any initial orbital to any other orbital .However this is not so because a photon a photon has as intrinsic spin angular momentum of √2h/2π corresponding to S=1 although it has no charge and no rest mass
On the other hand , an electron has got two type of angular momentum: orbital angular momentum
L=[√l(l+1)]h/2π,and spin angular momentum L1=√s(s+1)h/2π arising from orbital motion and spin motion of the electron during any electronic transition must compensate for the angular momentum carried away by the photon .To satisfy this condition the different between the azimuthal quantum number of the orbital within which the transition take place must differ by 1.thus, an electron in a d-orbital (l=2) cannot make a transition into as s-orbital (l=0)because the photon cannot carry away enough angular momentum
The maximum orbital angular momentum of an electron with n=5 is
View SolutionL=√l(l+1)h2π
On the other hand, m determines Z-component of orbital angular momentum as Lz=m(h2π)
Hund's rule states that in degenerate orbitals electron s do not pair up unless and until each such orbital has got an electron with parallel spins. Besides orbital motion, an electron also possess spin-motion. spin may be clockwise and anti-clockwise. Both thes spin motions are called two spin states of electron characterised by spin. s=+12 and s=−12, respectively.
The orbital angular momentum of electron (l=1) makes an angle of 45∘ from Z-axis. The Lz of electron will be
View Solution