The system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If partial vapour pressure of A is twice that of partial vapour pressure of B and total vapour pressure 2 atm at TK, where T=50K and V=8.21L, then the number of moles of A and B in vapour phase is:
83,43
43,13
23,14
103,43
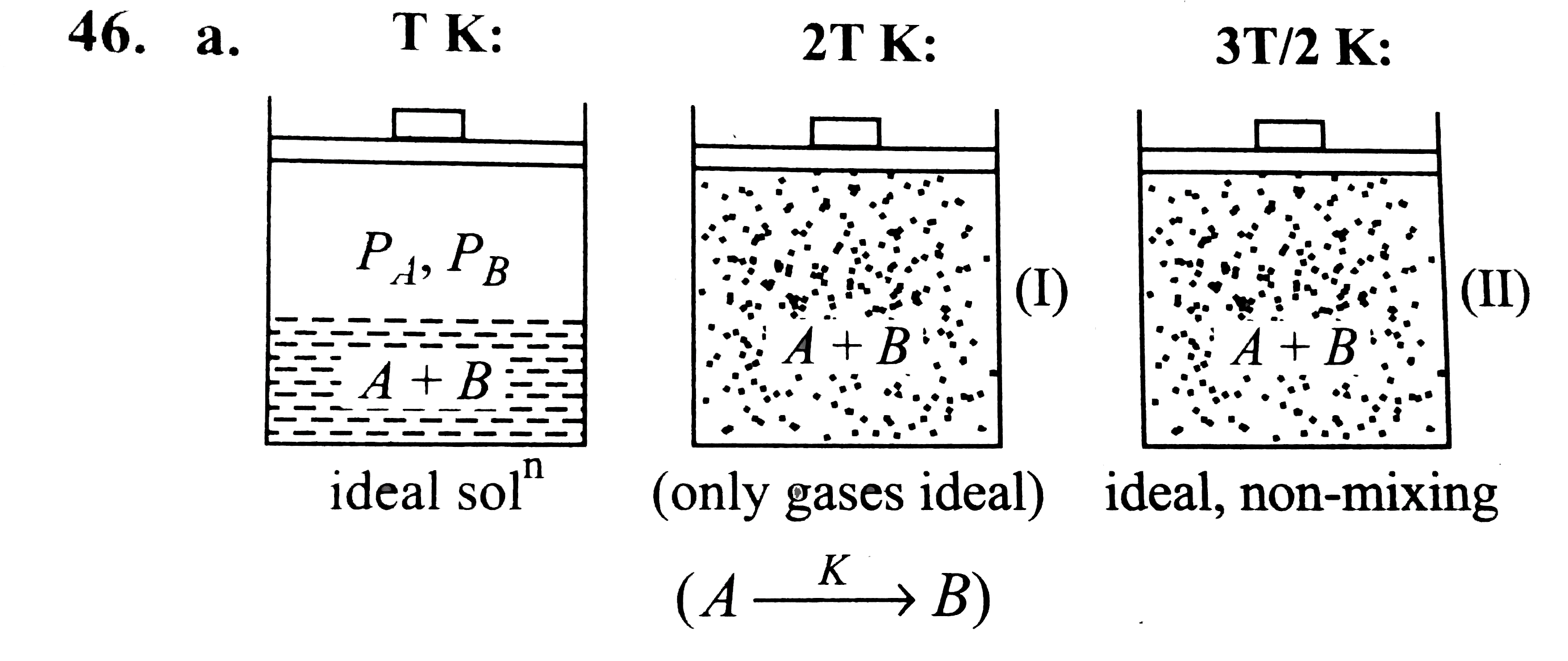
nAnB=PAPB=2, Total V.P.=2atm,
PV=nRT⇒2×8.21=(nA+nB)×0.0821×50
⇒nA+nB=4
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRYCHAPTER - STATES OF MATTEREXERCISE - Exercises (Multiple Correcttype)32videos
STATES OF MATTER
- BOOK - CENGAGE CHEMISTRYCHAPTER - STATES OF MATTEREXERCISE - Exercises (Single Correct)85videos
STATES OF MATTER
- BOOK - CENGAGE CHEMISTRYCHAPTER - STATES OF MATTEREXERCISE - Exercises21videos
STATES OF MATTER
- BOOK - CENGAGE CHEMISTRYCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective11videos
SOME BASIC CONCEPTS AND MOLE CONCEPT
- BOOK - CENGAGE CHEMISTRYCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective33videos
STOICHIOMETRY
Similar Questions
Which of the following statements is/are correct?
View SolutionAt what temperature will both celsius and fahrenheit scales read the same value?
View Solution100mL of gas is collected at 750mm pressure. What volume will it occupy at 74.5mm pressure?
03:05View SolutionWhat is the molarityk and molality of a 13% solution (by weight) of sulphric acid with a density of 1.02mL−1? To what volume should 100mL of this acid be diluted in order to preapre a 1.5N solution?
03:14View SolutionIn the analysis of 0.1 of sample of feldspar, 0.118 g of mixture of NaCl and KCl is obtained which on treatment with AgNO3 gives 0.2451 of AgCl. Calculate the precentage of Na2O and K2O in feldspar.
View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
Vapours of A and B are passed into a container of volume 8.21L, maintained at 2TK, where T=50K and after 5min, moles of B=8/3. The pressure developed into the cotainer after two half lives isView SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If vapours are collected in a container of volume 8.21L maintained at 3T/2K, where T=50K, then the ratio of initial rate of effusion of gases A and B is given asView SolutionVapour pressure of a solvent is the pressure exterted by vapour when they are in equilibrium with its solvent at that temperature. The vapour pressure of solvent is dependent of nature of solvent, temperature, addition of non-volatile solute as well as nature of solute to dissociate or associate. The vapour pressure of a mixture obtained by mixing two valatile liquids is given by PM=P∘A.XA+P∘B.XB where P∘A and P∘B are vapour pressures of pure components A and B and XA,XB are their mole fractions in mixture. For solute-solvent system, the relatio becomes PM=P∘A.XA where B is non-volatile solute.
If M is mol.wt. of solvent, Kb is molal elevation constant and tb is its boiling point, P∘ is its vapour pressure ta temperature T and PS is vapour pressure of non-volatile solute in it at TK, then:09:43View SolutionLiquid A and B form an ideal solution. At 25^(@)C . 5 moles of vapours of liquid 'A' and 10 moles of vapour of liquid B are taken in a cylinder piston arrangement and a pressure of 0.6 bar is maintained. At 25^(@)C , P_(A)^(@)=0.5 bar , P_(B)^(@) =1.0 bar. The only correct statement about the system is :
View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK.standard vapour pressure of A and B are P∘AandP∘B respectively at TK.We collect the vapour of A and B in two container of volume V, first container is maintained at 2TK and second container is maintained at 3T2K.At the temperature greater than TK, both A and B exist in only gaseous form.Total vapour pressure of the system at TK is given as
P=P∘AXA+P∘BXB
where XAandXB are the mole fraction of A and B in a liquid mixture.
In container (1)
We assume that collected gases behave ideally at 2TK and there can take place isomerisation reaction in which A converted into B by first order kinetics
Reaction is given as
AA−−→B
In container (II)
At the given temperature 3T2,A and B are ideal in nature and non mixing in nature.A small pin hole is made into container.We can determine the initial rate of effusion of both gases in vaccum by the expression
r=kp√m
Where P= pressure difference between system and surrounding
K=positibe constant
M=Molecular weight of the gas.

If partial vapour pressure of A is twice that of partial vapour pressure of B and total V.P. of equal to 2 at T=50 K and V=8.21 lit, then number of mole of A and B in vapour phase is :View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK.standard vapour pressure of A and B are P∘AandP∘B respectively at TK.We collect the vapour of A and B in two container of volume V, first container is maintained at 2TK and second container is maintained at 3T2K.At the temperature greater than TK, both A and B exist in only gaseous form.Total vapour pressure of the system at TK is given as
P=P∘AXA+P∘BXB
where XAandXB are the mole fraction of A and B in a liquid mixture.
In container (1)
We assume that collected gases behave ideally at 2TK and there can take place isomerisation reaction in which A converted into B by first order kinetics
Reaction is given as
AA−−→B
In container (II)
At the given temperature 3T2,A and B are ideal in nature and non mixing in nature.A small pin hole is made into container.We can determine the initial rate of effusion of both gases in vaccum by the expression
r=kp√m
Where P= pressure difference between system and surrounding
K=positibe constant
M=Molecular weight of the gas.
Vapour is collected and passed into a container of volume 8.21 lit, maintainer at 100 K and after 5 min number of mole of B=83.Then calculate pressure develop into the container after two half lives.View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK.standard vapour pressure of A and B are P_A^@ and P_B^@ respectively at TK.We collect the vapour of A and B in two container of volume V, first container is maintained at 2TK and second container is maintained at (3T)/2 K.At the temperature greater than TK, both A and B exist in only gaseous form.Total vapour pressure of the system at TK is given as P=P_A^@X_A+P_B^@X_B where X_A and X_B are the mole fraction of A and B in a liquid mixture. In container (1) We assume that collected gases behave ideally at 2TK and there can take place isomerisation reaction in which A converted into B by first order kinetics Reaction is given as AoversetAtoB In container (II) At the given temperature (3T)/2 ,A and B are ideal in nature and non mixing in nature.A small pin hole is made into container.We can determine the initial rate of effusion of both gases in vaccum by the expression r=(kp)/sqrtm Where P= pressure difference between system and surrounding K=positibe constant M=Molecular weight of the gas. If vapour is collected in container of volume 8.21 lit maintained at 75 K then ratio of initial rate of effusion of Gas A and B is given as :
View SolutionEqual volume of a liquid is poured into containers A and B where area of cross-section of container A is double the area of cross-section of container B. If PAandPB are pressures exerted at the bottom of the containers, then find PA:PB.
02:17View SolutionLiquids 'A' and 'B' form an ideal solution. If the mole- fraction of 'A' in liquid and vapour forms at equilibrium is 0.4 and 0.6, respectively, the value of P0AP0B is.
04:06View SolutionTwo liquids A and B are mixed at temperature T in a certain ratio to form an idela solution. It is found that the partial vapoure pressure of A. i.e, PA is equal to ps. The vapoure pressure of B for the liquid mixture. Whatis the total vapour pressure of the liquid mixture in terms of P∘AandP∘B ?
View Solution

