The value of PV for 5.6L of an ideal gas is ……… RT at NTP.
0.25
0.30
1.0
0.45
To solve the question regarding the value of PV for 5.6L of an ideal gas at NTP, we can follow these steps:
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
\( PV = nRT \)
where:
- \( P \) = pressure
- \( V \) = volume
- \( n \) = number of moles of gas
- \( R \) = universal gas constant
- \( T \) = temperature in Kelvin
Step 2: Determine the Volume of the Gas
We are given that the volume \( V = 5.6 \, L \).
Step 3: Find the Number of Moles of the Gas
At Normal Temperature and Pressure (NTP), 1 mole of an ideal gas occupies \( 22.4 \, L \). To find the number of moles \( n \) in \( 5.6 \, L \):
\(
n = \frac{V}{22.4 \, L} = \frac{5.6 \, L}{22.4 \, L} = \frac{1}{4} = 0.25 \, moles
\)
Step 4: Substitute Values into the Ideal Gas Law
Now substituting the value of \( n \) back into the ideal gas equation:
\(
PV = nRT = 0.25 \, moles \times RT
\)
Step 5: Express PV in Terms of RT
Thus, we can express \( PV \) as:
\(
PV = 0.25 \, RT
\)
Conclusion
Therefore, the value of \( PV \) for \( 5.6 \, L \) of an ideal gas at NTP is:
\(
PV = 0.25 \, RT
\)
Final Answer
The value of PV for 5.6L of an ideal gas is 0.25 RT.
---
The ideal gas law is given by the equation:
\( PV = nRT \)
where:
- \( P \) = pressure
- \( V \) = volume
- \( n \) = number of moles of gas
- \( R \) = universal gas constant
- \( T \) = temperature in Kelvin
We are given that the volume \( V = 5.6 \, L \).
At Normal Temperature and Pressure (NTP), 1 mole of an ideal gas occupies \( 22.4 \, L \). To find the number of moles \( n \) in \( 5.6 \, L \):
\(
n = \frac{V}{22.4 \, L} = \frac{5.6 \, L}{22.4 \, L} = \frac{1}{4} = 0.25 \, moles
\)
Now substituting the value of \( n \) back into the ideal gas equation:
\(
PV = nRT = 0.25 \, moles \times RT
\)
Thus, we can express \( PV \) as:
\(
PV = 0.25 \, RT
\)
Therefore, the value of \( PV \) for \( 5.6 \, L \) of an ideal gas at NTP is:
\(
PV = 0.25 \, RT
\)
The value of PV for 5.6L of an ideal gas is 0.25 RT.
Topper's Solved these Questions
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Assertion-Reasoning)
24 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Integer)
10 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Multiple Correcttype)
32 Videos
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective
11 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Knowledge Check
The graph of PV vs P for a gas is
AparabolicBhyperbolicCa straight line parallel to X-axisDa straight line passing through origin
The ideal gas equation for 1 mol of ideal gas is PV = nRT
graph between P and T at constant volume, i.e. isochores are plotted as under
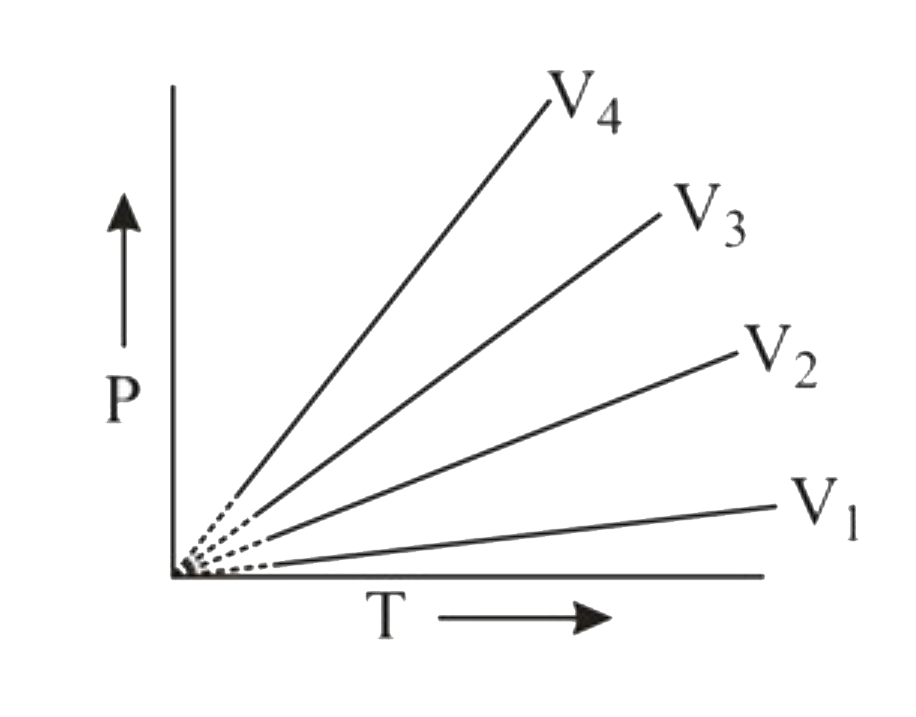
Which of the following order of volume is correct ?
View SolutionCompressibility factor, Z of a gas is given as Z=pVnRT
(i) What is the value of Z for an ideal gas ?
(ii) For real gas what will be the effect on value of Z above boyle's temperature ?
View SolutionPressure volume (PV) work done by an ideal gas system at constant volume is
View SolutionAssertion : Compressibility factor for ideal gas is one.
Reason : For an ideal gas PV=nRT equation is obeyed.
View SolutionIf the ratio of PVm&RT for a real gas is x24 at a temp where (∂P∂Vm)=0. The find value of 10x.
View SolutionThe internal energy of an ideal gas is sum of total kinetic energy of molecules. Consider an ideal gas in which the relation among U, P and V is U=2+3PVThe gas is
View SolutionIn the equation of state of an ideal gas PV =nRT , the value of the universal gas constant is not correct :
View Solution
