Pressure volume (PV) work done by an ideal gas system at constant volume is
−ΔPP
Zero
−VΔP
−ΔV
The correct Answer is:B
To solve the question regarding the pressure-volume (PV) work done by an ideal gas system at constant volume, we can follow these steps:
1. Understanding Work Done in Thermodynamics:
- The work done (W) by a gas during expansion or compression can be expressed as:
W=−PΔV
where P is the pressure and ΔV is the change in volume.
2. Identifying Conditions:
- The question specifies that the process occurs at constant volume. This means that the volume of the gas does not change during the process.
3. Determining Change in Volume:
- Since the volume is constant, the change in volume (ΔV) is:
ΔV=Vfinal−Vinitial=0
4. Substituting into the Work Formula:
- Substituting ΔV=0 into the work formula gives:
W=−P×0=0
5. Conclusion:
- Therefore, the work done by an ideal gas system at constant volume is:
W=0
Final Answer:
The pressure-volume (PV) work done by an ideal gas system at constant volume is zero.
---
- The work done (W) by a gas during expansion or compression can be expressed as:
W=−PΔV
where P is the pressure and ΔV is the change in volume.
- The question specifies that the process occurs at constant volume. This means that the volume of the gas does not change during the process.
- Since the volume is constant, the change in volume (ΔV) is:
ΔV=Vfinal−Vinitial=0
- Substituting ΔV=0 into the work formula gives:
W=−P×0=0
- Therefore, the work done by an ideal gas system at constant volume is:
W=0
The pressure-volume (PV) work done by an ideal gas system at constant volume is zero.
Topper's Solved these Questions
Similar Questions
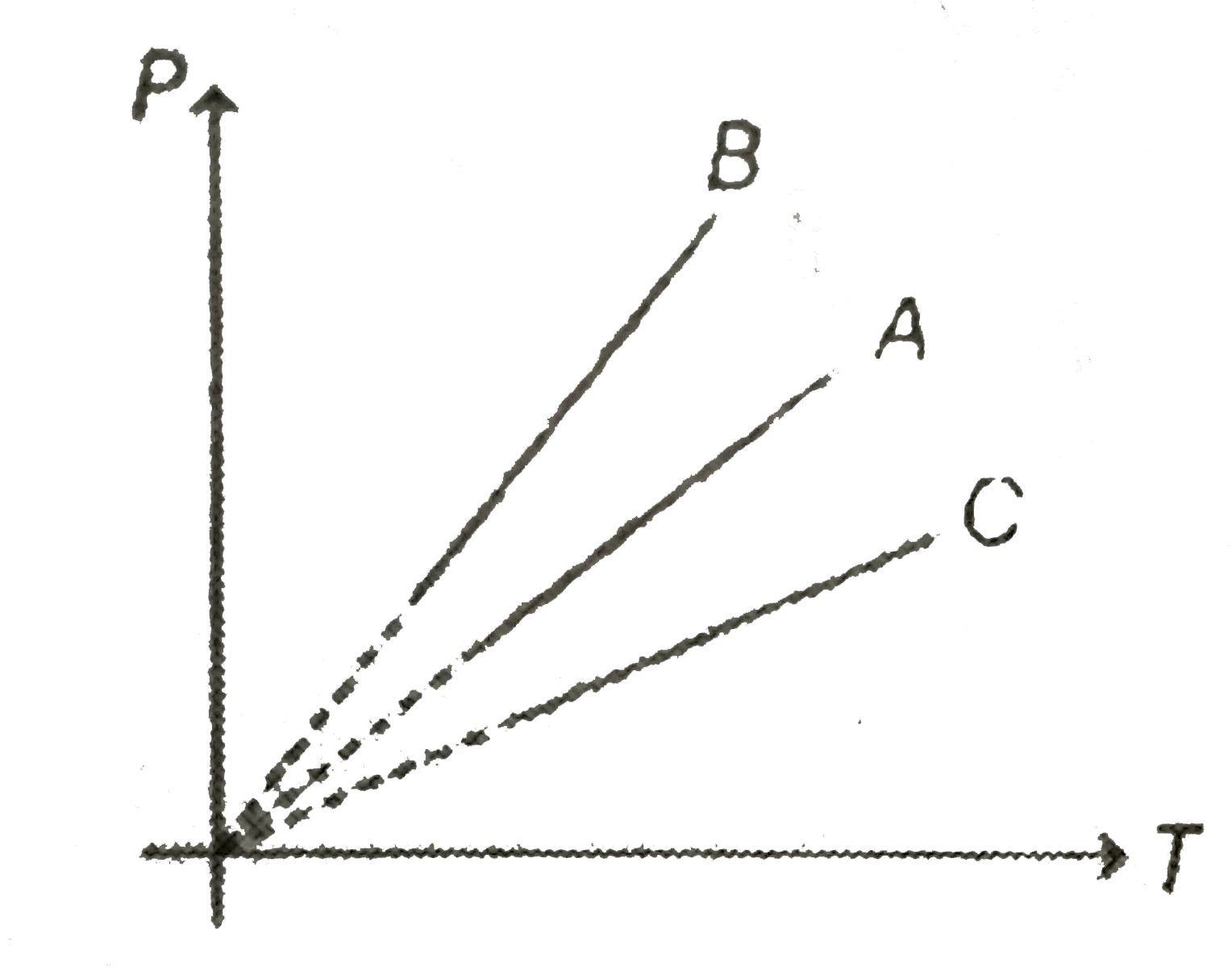
Pressure versus temperature graph of an ideal gas at constant volume V is shown by the straight line A. Now mass of the gas is doubled and the volume is halved, then the corresponding pressure versus temperature graph will be shown by the line
View SolutionCp is always greater than Cv for a gas, which of the following statements provide, partly or wholly, the reason for this?
(i) No work is done by a gas at constant volume
(ii) When a gas absorbs heat at constant pressure, its volume must change
(iii) For the same change in temperature, the internal energy of a gas changes by a smaller amount at constant volume that at constant pressure
(iv) The internal energy of an ideal gas is a function only of its temperature
View SolutionStatement-1: For a gaseous system Cp is always greater than Cv
Statement-2: Work done by a gas at constant volume is zero.
View SolutionAn ideal gas intially has pressure P volume V and temperature T. Its is isothermally expanded to four times of its original volume, then it is compressed at constant pressure to attain its original volume V. Finally, the gas is heated at constant volume to get the original temperature T. (a) Draw V−T curve (b) Calculate the total work done by the gas in the process.(given ln2=0.693)
View SolutionThree moles of an ideal gas (Cp=72R) at pressure, PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally gas is compressed at constant volume to its original pressure PA.
(a) Sketch P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
View SolutionThe figures given below show different processes (relating pressure P and volume V) for a given amount of an ideal gas. W is work done by the gas and ΔQ is heat absorbed by the gas.
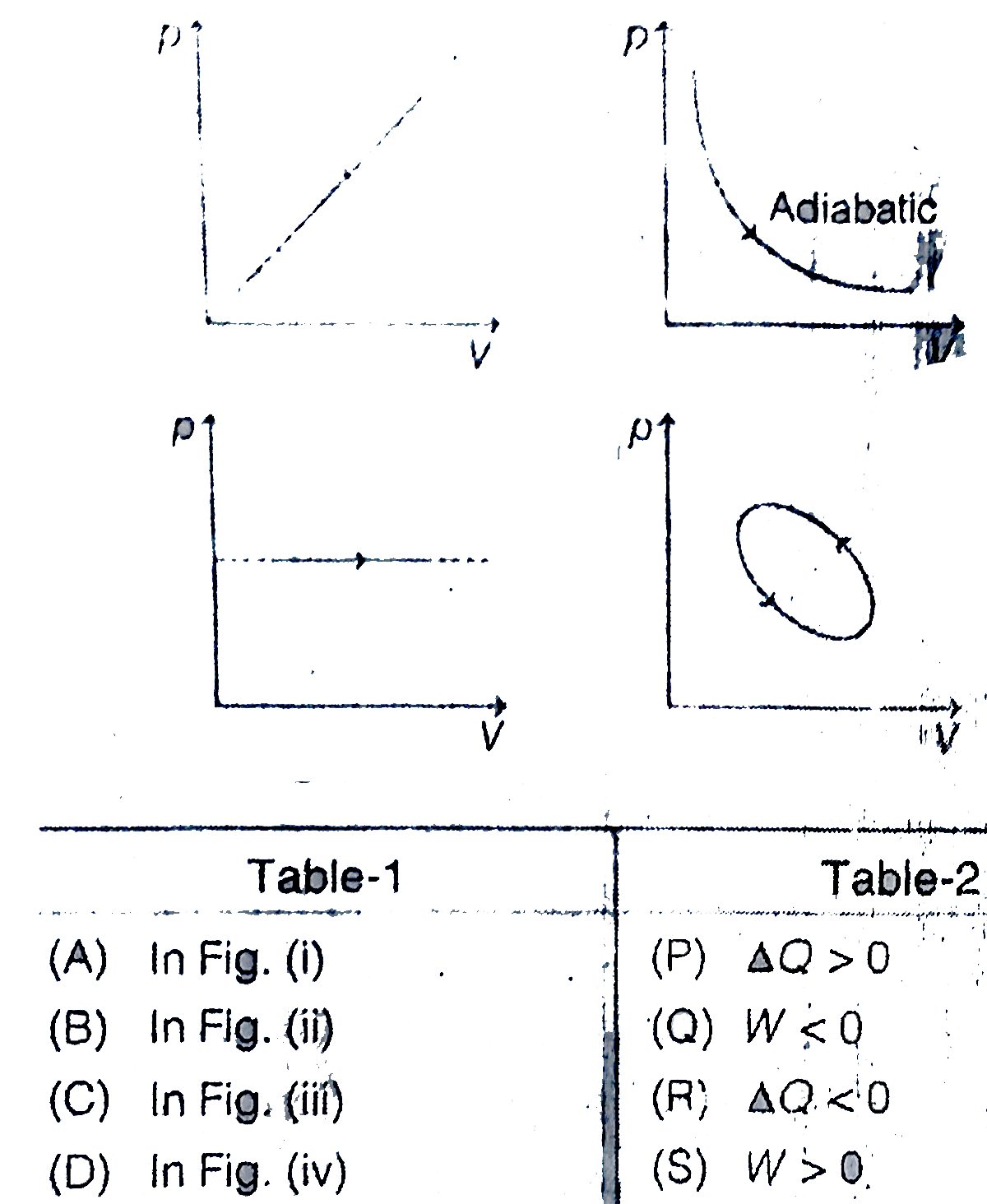
View SolutionIf the pressure of an ideal gas at constant volume is decreased by 20% then the percentage change in temperature will be
View SolutionThree moles of an ideal gas at a pressure PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original , volume. Finally the gas is compressed at constant volume to its original pressure PA
(a) Sketch the P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
View SolutionA diatomic ideal gas is heated at constant volume until the pressure is doubled and again heated at constant pressure until the volume is doubled. The average molar heat capacity for the whole process is
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View Solution
