Three students measured the focal length of a convex lens using parallel rays from distant object. All of the measured the distance between the lens and the inverted image on the screen. Student A saw a sharp image on the screen and labelled the distance as f1. Student B saw a slightly larger blurred image on the screen and labelled the distance as f2. Student C saw a slightly smaller blurred image on the screen and labelled the distance as f3 . What is the relation between the three measurements?
A sharp image is formed at focus. A slightly blurred larger image is formed beyond the focus and a slightly blurred smaller image is formed before the focus.
Therefore, f3<f1<f2).
Topper's Solved these Questions
- PRACTICAL BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - PRACTICAL BASED QUESTIONSEXERCISE - Experiment 11
4 Videos
- PRACTICAL BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - PRACTICAL BASED QUESTIONSEXERCISE - Experiment 12
6 Videos
- PRACTICAL BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - PRACTICAL BASED QUESTIONSEXERCISE - Experiment 9
4 Videos
- PERIODIC CLASSIFICATION OF ELEMENTS BOOK - VK GLOBAL PUBLICATIONCHAPTER - PERIODIC CLASSIFICATION OF ELEMENTS EXERCISE - PROFICIENCY EXERCISE (LONG ANSWER QUESTIONS)
3 Videos
- VALUE-BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - EXERCISE (CHAPTER-16) MANAGEMENT OF NATURAL RESOURCES
9 Videos
Similar Questions
A student measures the focal length of a convex lens by putting an object pin at a distance u from the lens and measuring the distance v of the image pin. The graph between u and v plotted by the student should look like
View SolutionTo find the focal length of a convex lens, an image of a far located tree is obtained on a screen. For this the distance measured is:
View Solution
Knowledge Check
Three students measured the focal length of a convex lens using parallel rays from a distant object. All of the measured the distance between the lens and the inverted image on the screen.
(i) Student A saw a sharp image on the screen and labelled the distance as f1
(ii) Student B saw a slightly larger blurred image on the screen and labelled the distance as f2
(iii) Student C saw slightly smaller blurred image on the screen and labelled the distance as f3
The relation between the three measurements would most likely be :Af1=f2=f3Bf1<f2<f3Cf3<f1<f2Df1<f2 and f1=f3A student measures the focal length of a convex lens by putting an object pin at a distance u from the lens and measuring the distance v of the image pin. The graph between u and v plotted by the student should look like
A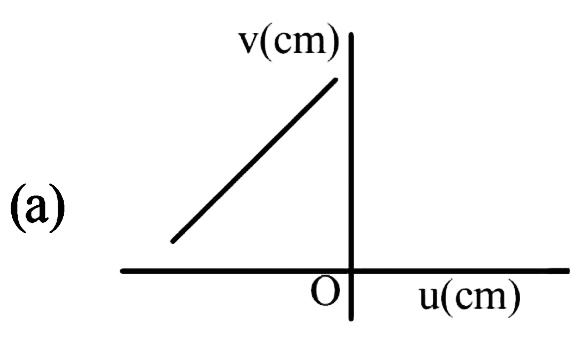 B
B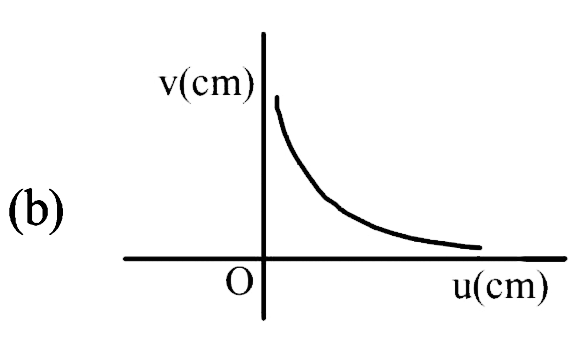 C
C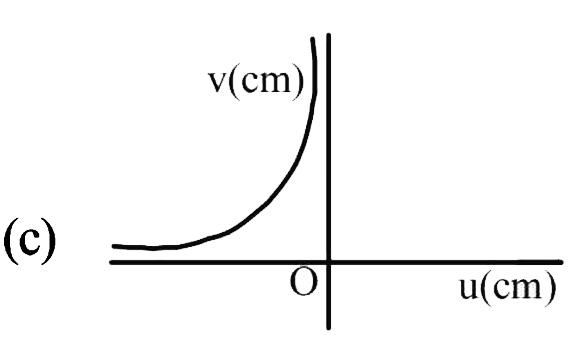 D
D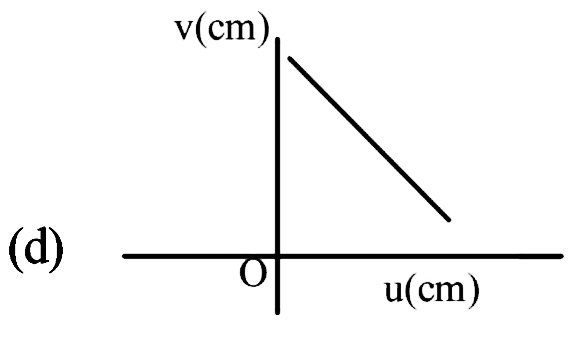
Parallel rays from a distant object incident on a convex lens form an image on the screen. The diagram showing correctly the image of the object on the screen is
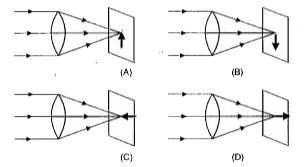 AABBCCDD
AABBCCDD
A student performs an experiment to estimate the focal length of a convex lens by obtaining the image of a distant window on a white screen. The image formed on the white screen is :
View SolutionWhile determining the focal length of a concave mirror, a student obtained the image of a distant object on a screen. In order to get the focal length of the mirror, the student should measure the distance :
View SolutionA student obtains a blurred image of a distant object on a screen using a convex lens. To obtain a distinct image on the screen he should move the lens
View SolutionA student obtains a blurred image of a distant object on a screen using a convex lens. To obtain a distinct image on the screen he should move the lens
View SolutionA student obtains a blurred image of a distant object on a screen using a convex lens. To obtain a distinct image on the screen he should move the lens
View Solution
