A student measures the focal length of a convex lens by putting an object pin at a distance u from the lens and measuring the distance v of the image pin. The graph between u and v plotted by the student should look like
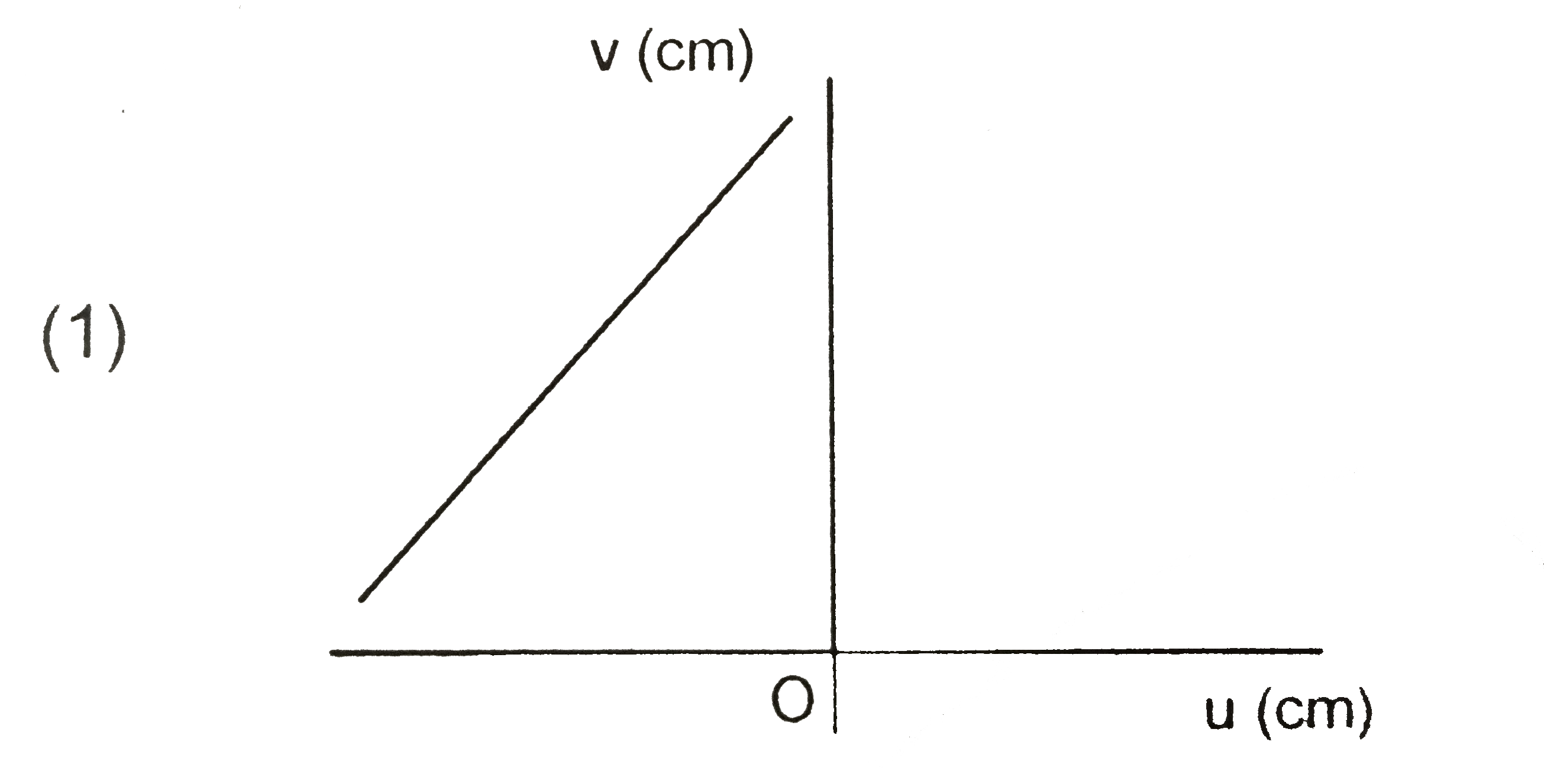
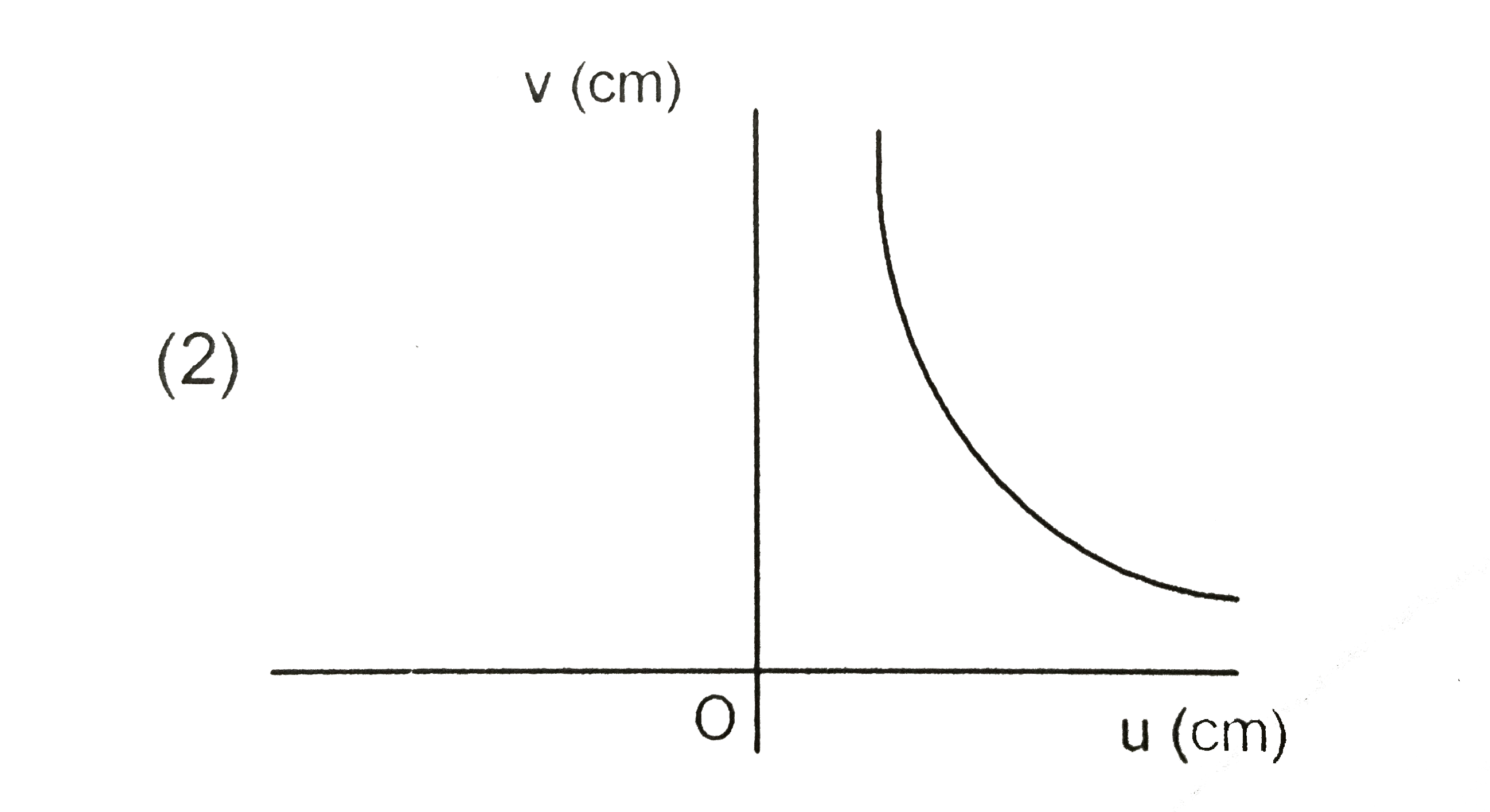
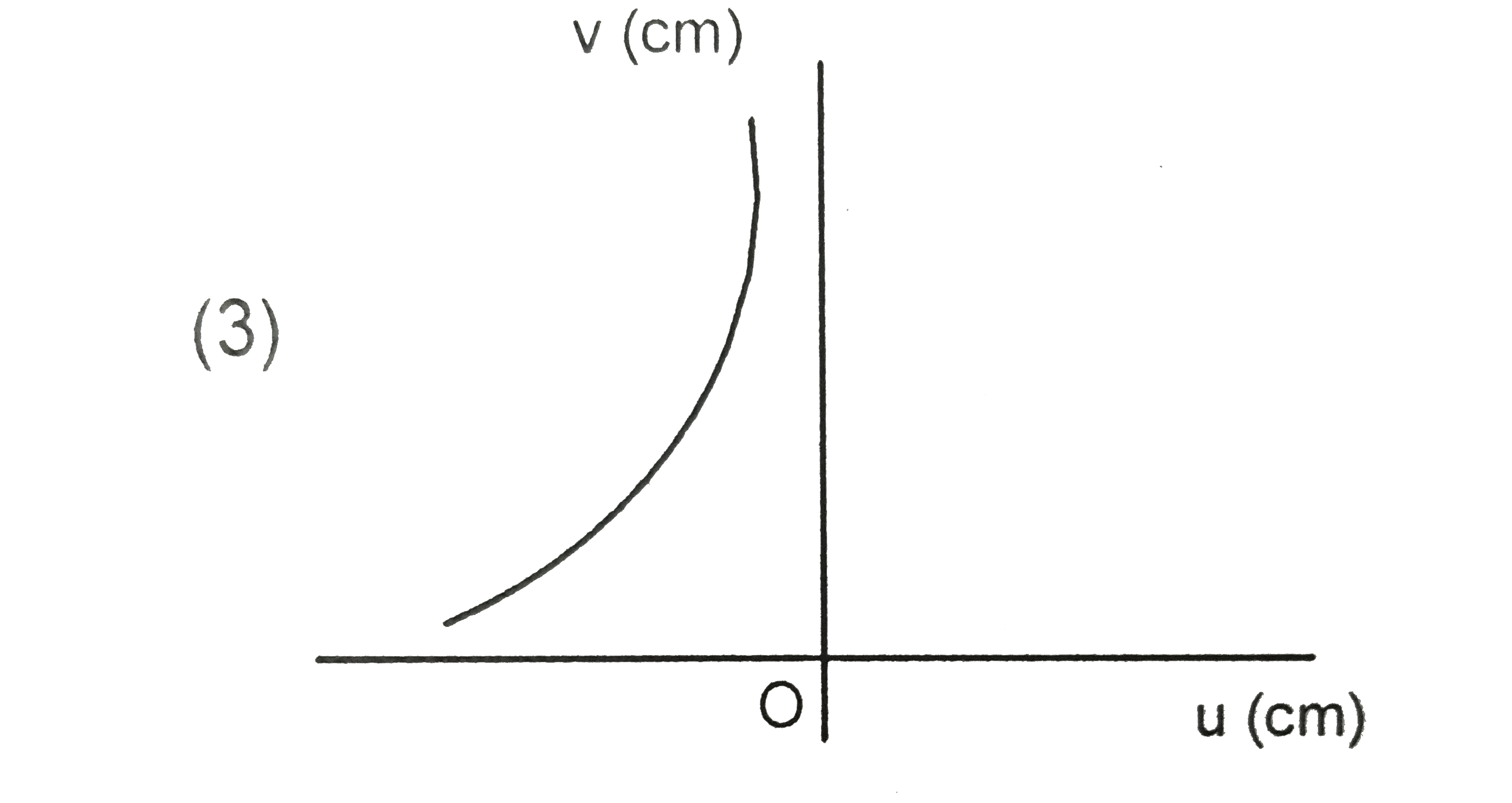
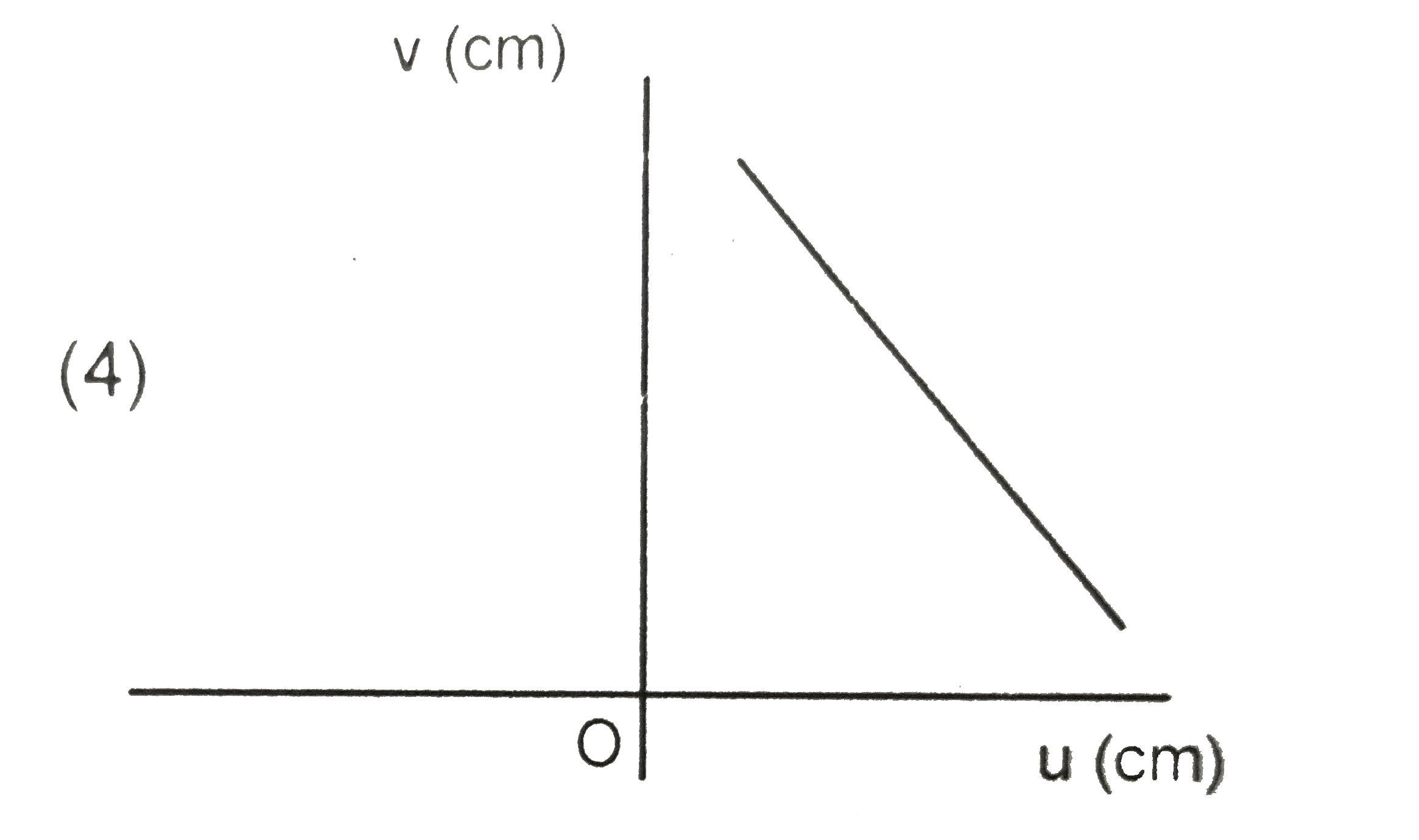
The correct Answer is:C
To determine the graph between the object distance u and the image distance v for a convex lens, we can start from the lens formula:
1f=1v−1u
Rearranging this formula gives us:
1v=1f+1u
Multiplying through by uv to eliminate the fractions results in:
u+v=uvf
From this equation, we can express v in terms of u:
v=fuu−f
This equation indicates that v is a function of u.
1. Identify the lens formula: Start with the lens formula, which relates the object distance u, image distance v, and focal length f.
1f=1v−1u
2. Rearrange the lens formula: Rearranging gives us 1v=1f+1u.
3. Multiply through by uv: To eliminate the fractions, multiply through by uv:
u+v=uvf
4. Express v in terms of u: Rearranging the equation gives:
v=fuu−f
5. Analyze the graph: The equation v=fuu−f indicates that as u approaches f, v approaches infinity (vertical asymptote). For u<f, v becomes negative, indicating that the image is virtual. For u>f, v is positive, indicating a real image. Thus, the graph will be a hyperbola.
6. Determine the quadrant: Since u is positive and v can be both positive and negative, the graph will lie in the second quadrant (where u is positive and v can be negative).
Conclusion:
The graph between u and v will be a hyperbola situated in the second quadrant.
1f=1v−1u
u+v=uvf
v=fuu−f
The graph between u and v will be a hyperbola situated in the second quadrant.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
An object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionIn an experiment for the determination of focal length of the convex mirror a convex lens of focal length 20cm is placed on the optical bench and an object pin is placed at a distance 30cm from the lens. When a convex mirror is introduced in between the lens and the real and inverted image of the object, the final image of object O is formed at O itself. If the distance between the lens and the mirror is 10cm, then the focal length of the mirror is
View SolutionAn extended object is placed at a distance of 5.0 cm from a convex lens of focal length 8.0 cm. (a) Draw the ray diagram (to the scale) to locate the image and from this, measure the distance of the image from the lens, (b) Find the position of the image from the lens formula and see how close the drawing is to the correct result.
View SolutionDraw a labelled ray diagram for the formation of image by a convex lens of focal length 15 cm when the object is placed at a distance of 25 cm from the lens. Determine the size of the image formed, if size of the object is 4 cm.
View SolutionA convex lens produces a real image m times the size of the object. What will be the distance of the object from the lens ?
View Solution
