Which of the following types of octahedral complexes can show mer-fac isomerism ?
where M is central metal, A, B and c are different monodentate ligands while AA is a symmetrical bidentate ligand.
A
or
B
or
C
D
Text Solution
The correct Answer is:C
Two diastereoisomers are possible for an octahedral complex of the type
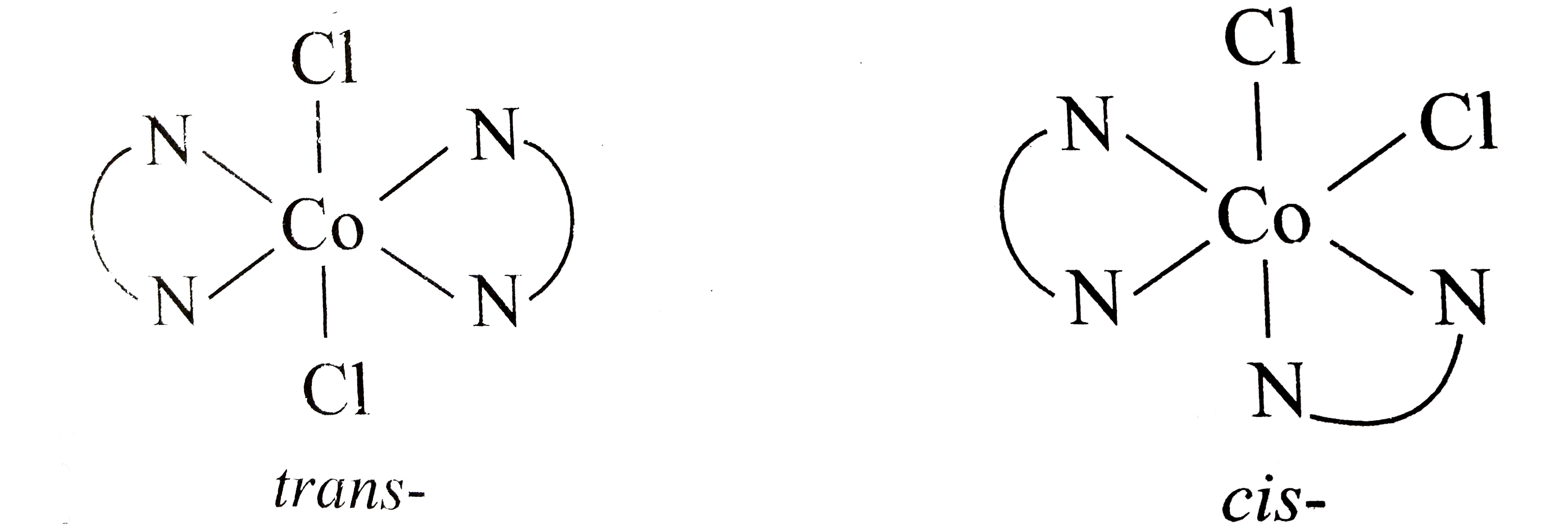
Note that two of the A ligands occupy positions just opposite one another. The four ligands have a square planar arrangement in which cis-trans isomers are possible. Two diastereoisomers are also possible for an octachedral complex of the type or as illustrated in Q.2. Octahedral complexes with the general formula exhibit mer-fac isomerism. If we first draw an A ligand and a B ligand opposite one another in an octahedral geometry. Then the other ligands can have cis or trans arrangements on the plane perpendicular toi the axis of the first A and B ligands:
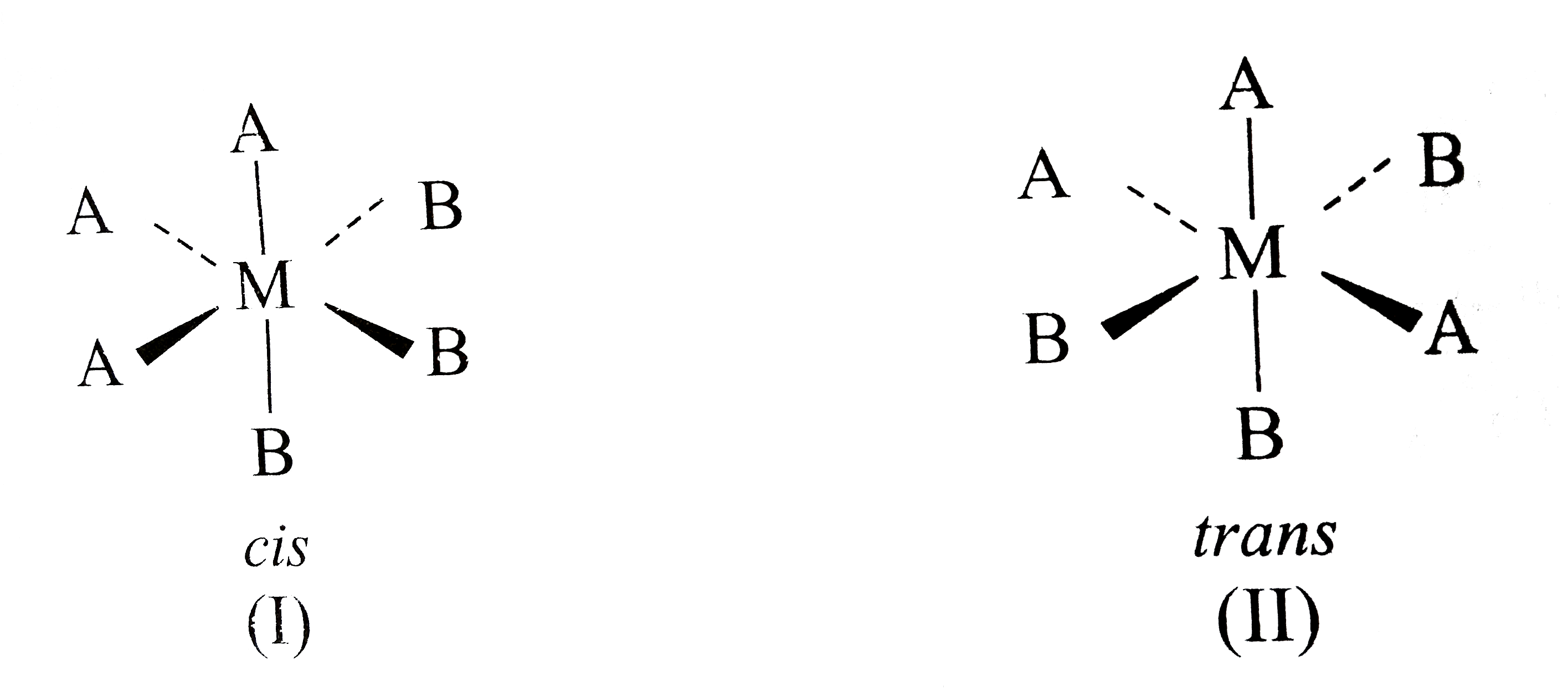
Isomer (I) show above has the three A ligands in adjacent positions ( separation) on one triangular face of the octahedron (fac-isomer), isomer (II) has all three A ligands in a plane that contains the M (mer-isomer). In isomer (I), all three B-M-B bonds angles are whereas in isomer (II) two B-M-B angles are and the third is . To convince ourselves that only two diasterosiomers of exist, look back at the cis-and trans- and consoider the products obtained form them when one of the four A ligands in cis-isomer is replaced by a B. There are two kinds of A-ligands in the cis-isomer: two A ligands that are trans to each other and two A ligands that are trans to a B ligands. Replacing an A trans to another A with B gives isomer (I), whereas replacing an A trans to a B with another B gives isomer (II)
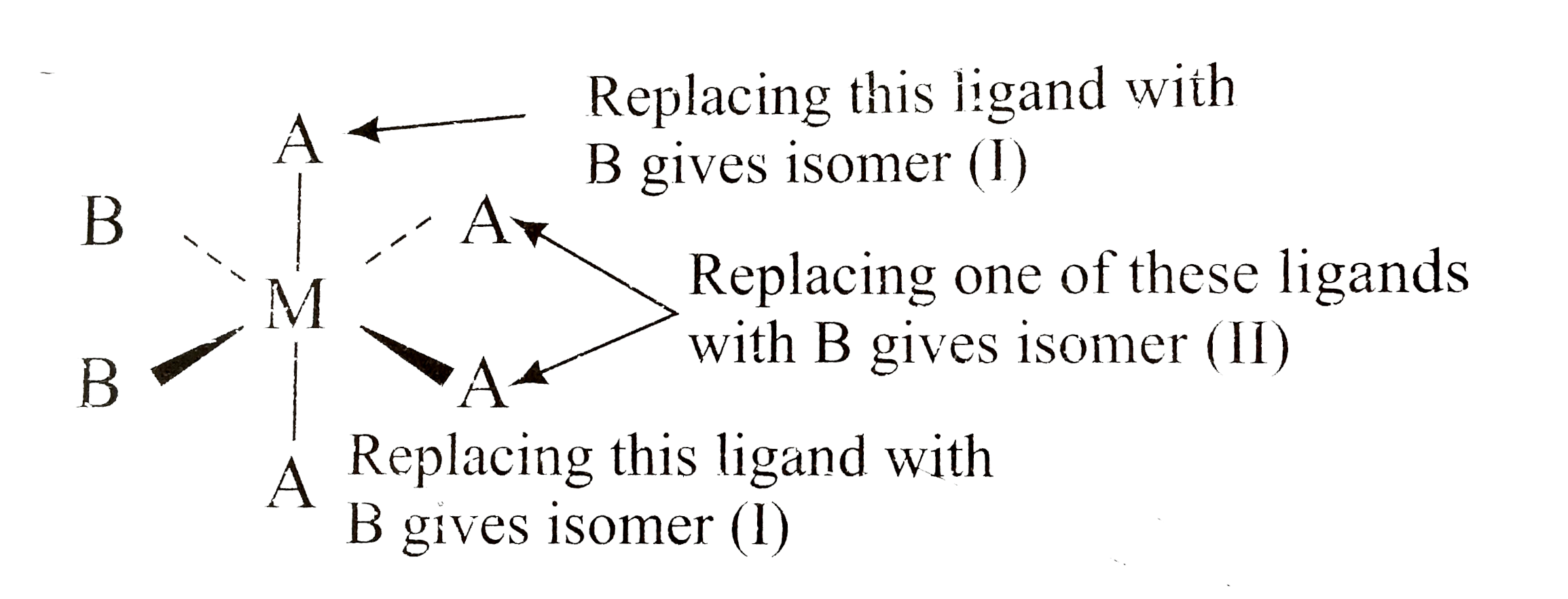
All four A ligands in trans - are equivalent, and replacing any one of them with a B gives isomer (II).

If we rotate the resulting complex, we can see that it is identical to the previous drawing of isomer (II). Thus, there are only two diasteroisomers for a complex of the type . Octahedral complexes of the type or would not show geometrical isomerism.
|
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - R SHARMACHAPTER - COORDINATION COMPOUNDSEXERCISE - Question Bank (Building the knowledge)
38 Videos
- COORDINATION COMPOUNDSBOOK - R SHARMACHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives
56 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - R SHARMACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Archives
11 Videos
- ELECTROCHEMISTRYBOOK - R SHARMACHAPTER - ELECTROCHEMISTRYEXERCISE - Follow-up Test 11
7 Videos
Similar Questions
Knowledge Check
Which of the following types of octahedral complexes does not show optical isomerism ?
AM(aa)2xyB[M(aa)3]C[M(aa)2x2]n+D[Ma5b]Which of the following types of octahedral complexes does not show optical isomerism ?
AMA2X2Y2B[M(AA)3]n+C[M(AA)2X2]n+D[Pt(NH)3)4]2+Which of the following types of octahedral complexes does not show optical isomerism?
A(a) MA2X2Y2B(b) [Pt(NH)3)4]2+C(c) [M(AA)3]n+D(d) [M(AA)2X2]n+
Which of the following types of square planer complexes has maximum number of geometric isomer ?
where Mn is central metal, A, B, C and D are different monodentate ligands, and AB is an unsymmetrical bidentate ligand.
View SolutionWhich one of the following octahedral complexes will not show geometrical isomerism ? (A and B are monodentate ligands)
View SolutionWhich one of the following octahedral complexes will not show geometrical isomerism ? (A and B are monodentate ligands)
View SolutionWhich of the following octahedral complex does not show geometrical isomerism (A and B are monodentate ligands) ?
View SolutionWhich of the following is optically inactive ?
[Where a, b =monodentate ligands, AA = symmetrical bidentate ligand]
View Solution
