A 0.6 C of charge is placed at right angled vertex B of a right angle triangle. Calculate the potential at point A and C, if AB = 3 cm and BC = 4 cm. Also calculate the work done in slowly moving a -0.1 μC charge from point A to C.
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry of the Triangle
We have a right-angled triangle with:
- Vertex B at the right angle
- AB = 3 cm
- BC = 4 cm
- Therefore, AC can be calculated using the Pythagorean theorem.
Step 2: Calculate the Distance AC
Using the Pythagorean theorem:
AC=√AB2+BC2=√(3cm)2+(4cm)2=√9+16=√25=5cm
Step 3: Convert Units to Meters
Since we need to use SI units for calculations, we convert the distances from centimeters to meters:
- AB = 0.03 m
- BC = 0.04 m
- AC = 0.05 m
Step 4: Calculate the Potential at Point A (VA)
The formula for electric potential V due to a point charge Q at a distance r is given by:
V=14πϵ0⋅Qr
Where:
- Q=0.6C
- r=AB=0.03m
- ϵ0=8.85×10−12C2/N m2
Calculating VA:
VA=14π(8.85×10−12)⋅0.60.03
Calculating the constant:
14π(8.85×10−12)≈9×109N m2/C2
Now substituting:
VA=9×109⋅0.60.03=9×109⋅20=1.8×1011V
Step 5: Calculate the Potential at Point C (VC)
Using the same formula for point C:
VC=14πϵ0⋅QBC
Where r=BC=0.04m:
VC=9×109⋅0.60.04=9×109⋅15=1.35×1011V
Step 6: Calculate the Work Done in Moving Charge from A to C
The work done W in moving a charge q through a potential difference V is given by:
W=q⋅(VC−VA)
Where:
- q=−0.1μC=−0.1×10−6C
- VC−VA=1.35×1011−1.8×1011=−0.45×1011
Calculating the work done:
W=−0.1×10−6⋅(−0.45×1011)=4.5×10−6J
Summary of Results
- Potential at point A VA=1.8×1011V
- Potential at point C VC=1.35×1011V
- Work done in moving the charge from A to C W=4.5×10−6J
We have a right-angled triangle with:
- Vertex B at the right angle
- AB = 3 cm
- BC = 4 cm
- Therefore, AC can be calculated using the Pythagorean theorem.
Using the Pythagorean theorem:
AC=√AB2+BC2=√(3cm)2+(4cm)2=√9+16=√25=5cm
Since we need to use SI units for calculations, we convert the distances from centimeters to meters:
- AB = 0.03 m
- BC = 0.04 m
- AC = 0.05 m
The formula for electric potential V due to a point charge Q at a distance r is given by:
V=14πϵ0⋅Qr
Where:
- Q=0.6C
- r=AB=0.03m
- ϵ0=8.85×10−12C2/N m2
VA=14π(8.85×10−12)⋅0.60.03
Calculating the constant:
14π(8.85×10−12)≈9×109N m2/C2
Now substituting:
VA=9×109⋅0.60.03=9×109⋅20=1.8×1011V
Using the same formula for point C:
VC=14πϵ0⋅QBC
Where r=BC=0.04m:
VC=9×109⋅0.60.04=9×109⋅15=1.35×1011V
The work done W in moving a charge q through a potential difference V is given by:
W=q⋅(VC−VA)
Where:
- q=−0.1μC=−0.1×10−6C
- VC−VA=1.35×1011−1.8×1011=−0.45×1011
W=−0.1×10−6⋅(−0.45×1011)=4.5×10−6J
- Potential at point A VA=1.8×1011V
- Potential at point C VC=1.35×1011V
- Work done in moving the charge from A to C W=4.5×10−6J
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 3
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 4
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 1
10 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
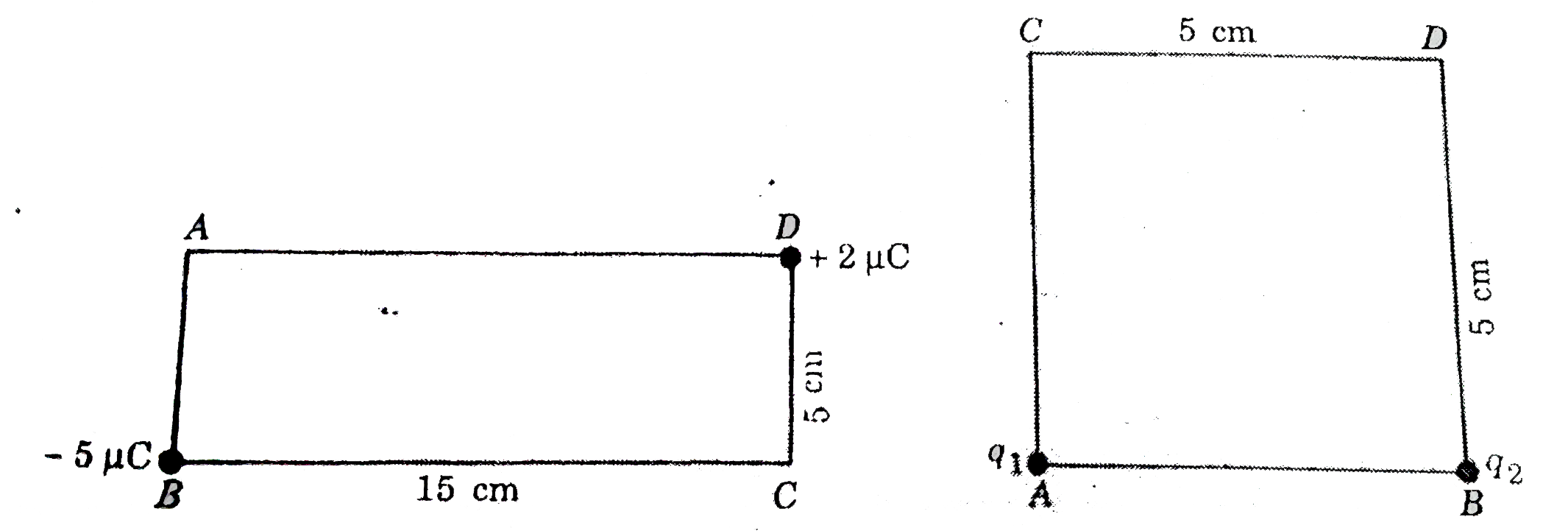
The sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of −5μC and +2μC are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of 3μC from A to C.
View SolutionCalculate the potential at point (0, 7 cm) due to a point charge of 0.2 μC placed at (0, 2 cm).
View Solution
Knowledge Check
If ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B6AC2C5AC2D54AC2In ΔABC, angle B is right angle, AB = 12 cm and BC = 5 m. The value of sin C is :
A1213B513C125D512Calculate the amount of work done to carry 4C of charge from a point at 100V to a point at 120V.
A80JB100JC5JD120J
In a right angled triangle ABC, the angle A is 90∘. What is the value of secB, if BC is 5 cm and AB is 3 cm
View SolutionConstruct a right-angled triangle ABC in which ∠A=90∘, BC=6cm and AB=4.8cm.
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionA right triangle ABC, right angled at A, is circumscribing a circle. If AB = 8 cm and BC = 6 cm, find the radius of the circle.
View SolutionIn a right angled triangle, with angle of A being right angle, the side AB is of length 4 cm and BC is 15 cm. What is the length of side AC?
View Solution
