A 1kg solid sphere rolls without slipping on a rough horizontal surface under the influence of a 7N force. The force acts tangentially at the highest point of the sphere. Which of the following statements are correct? (7N force acts towards right).
The frictional force on the sphere acts towards right.
The value of the frictional force is 3N
The acceleration of the centre of the sphere is 9.8m/s2
The acceleration of the centre of the sphere is 10m/s2
The correct Answer is:A, B, D
To solve the problem, we need to analyze the forces acting on the solid sphere and apply Newton's laws of motion. Let's break it down step by step.
Step 1: Identify the Forces Acting on the Sphere
The forces acting on the sphere are:
- A tangential force F=7N acting to the right at the highest point of the sphere.
- A frictional force f acting to the left at the point of contact with the ground.
Step 2: Write the Equations of Motion
Since the sphere rolls without slipping, we can apply Newton's second law for translation and rotation.
1. Translational Motion:
F−f=ma
where m=1kg and a is the linear acceleration of the center of mass.
2. Rotational Motion:
The torque τ about the center of mass due to the forces is given by:
τ=F⋅r−f⋅r=Iα
where I is the moment of inertia of the sphere and α is the angular acceleration. For a solid sphere, the moment of inertia is:
I=25mr2
Since α=ar (due to rolling without slipping), we can substitute α into the torque equation.
Step 3: Substitute Values into the Equations
Substituting the values into the equations:
1. From the translational motion:
7−f=1⋅a(1)
2. From the rotational motion:
7⋅r−f⋅r=25mr2⋅ar
Simplifying gives:
7−f=25a(2)
Step 4: Solve the Equations
Now we have two equations:
1. 7−f=a (from equation 1)
2. 7−f=25a (from equation 2)
From equation (1), we can express a in terms of f:
a=7−f
Substituting this into equation (2):
7−f=25(7−f)
Step 5: Solve for f
Multiplying through by 5 to eliminate the fraction:
5(7−f)=2(7−f)
Expanding gives:
35−5f=14−2f
Rearranging terms:
35−14=5f−2f
21=3f
Thus, we find:
f=7N
Step 6: Calculate the Acceleration
Substituting f back into equation (1):
7−7=a⟹a=0m/s2
Conclusion
The sphere does not accelerate, and the friction force acts to the left. The correct statements based on our calculations are:
- The acceleration of the sphere is 0m/s2.
- The friction force acts to the left.
The forces acting on the sphere are:
- A tangential force F=7N acting to the right at the highest point of the sphere.
- A frictional force f acting to the left at the point of contact with the ground.
Since the sphere rolls without slipping, we can apply Newton's second law for translation and rotation.
F−f=ma
where m=1kg and a is the linear acceleration of the center of mass.
The torque τ about the center of mass due to the forces is given by:
τ=F⋅r−f⋅r=Iα
where I is the moment of inertia of the sphere and α is the angular acceleration. For a solid sphere, the moment of inertia is:
I=25mr2
Since α=ar (due to rolling without slipping), we can substitute α into the torque equation.
Substituting the values into the equations:
1. From the translational motion:
7−f=1⋅a(1)
7⋅r−f⋅r=25mr2⋅ar
Simplifying gives:
7−f=25a(2)
Now we have two equations:
1. 7−f=a (from equation 1)
2. 7−f=25a (from equation 2)
a=7−f
7−f=25(7−f)
Multiplying through by 5 to eliminate the fraction:
5(7−f)=2(7−f)
Expanding gives:
35−5f=14−2f
Rearranging terms:
35−14=5f−2f
21=3f
Thus, we find:
f=7N
Substituting f back into equation (1):
7−7=a⟹a=0m/s2
The sphere does not accelerate, and the friction force acts to the left. The correct statements based on our calculations are:
- The acceleration of the sphere is 0m/s2.
- The friction force acts to the left.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative
 View Solution
View SolutionA metal sphere is hung by a string fixed to a wall. The forces acting on the sphere are shown in fig Which of the following statements are correct?
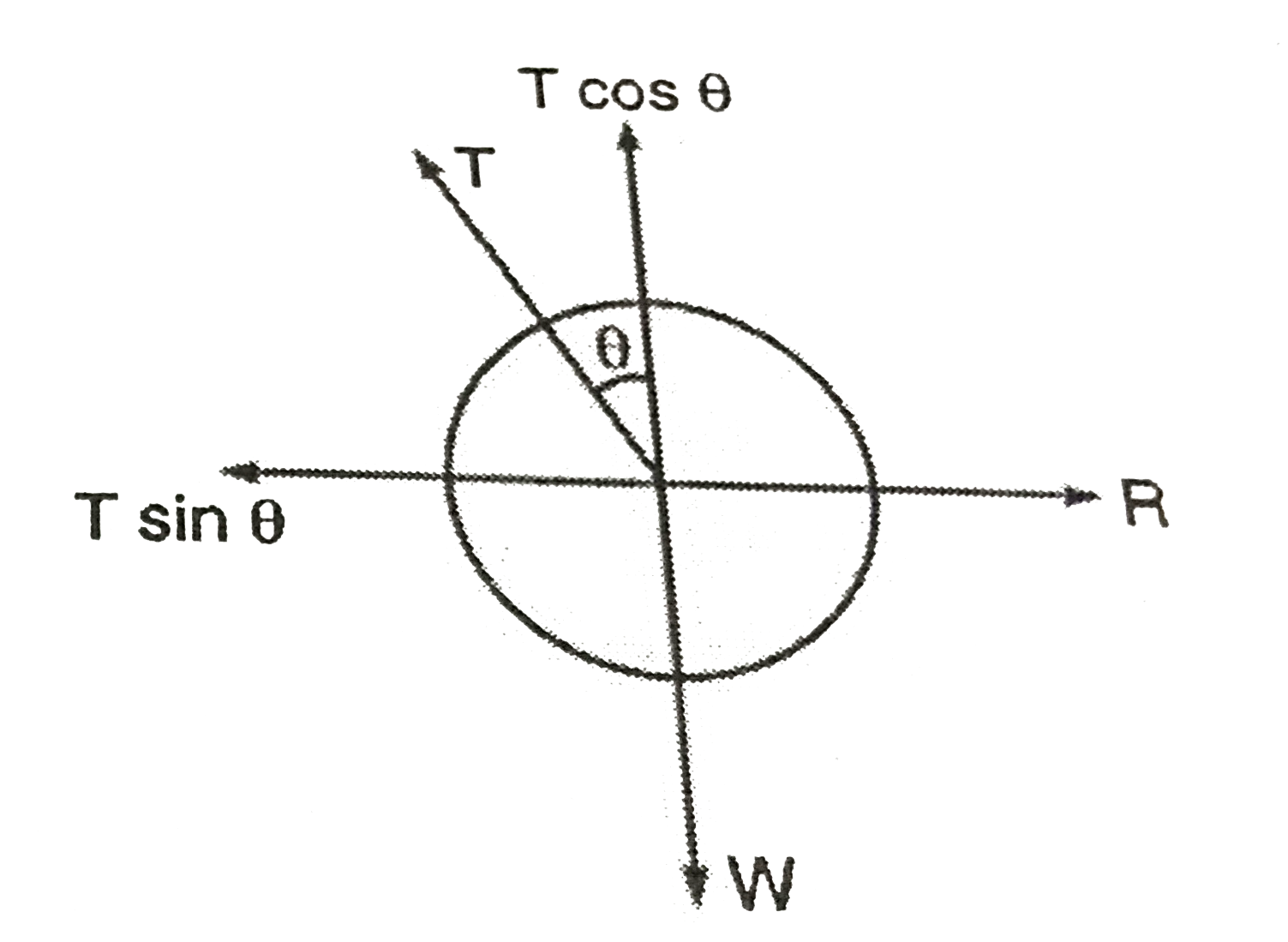 View Solution
View SolutionA 10kg solid sphere of radius r=0.8m is rolling without slipping on a horizontal rough surface with 8m/s. The force applied by the right half of the sphere on the left half is 30x. Newton. Find the value of x.
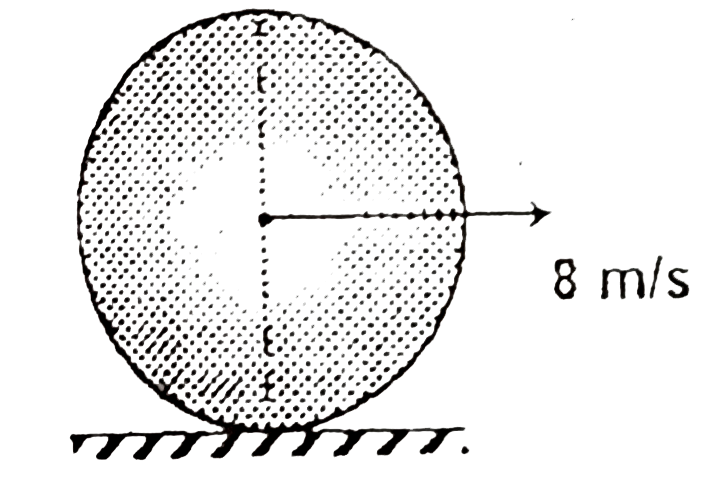 View Solution
View Solution
A spool is pulled horizontally on rough surface by two equal and opposite forces as shown in the figure. Which of the following statements are correct?View SolutionA sphere is rolled on a rough horizontal surface. It gradually slows down and stops. The force of friction tries to
View SolutionTwo small spheres of equal mass, and heading towards each other with equal speeds, undergo a head on collision ( external force acts on system of two spheres ). Then which of the following statement is correct ?
View SolutionA metal sphere is hung by a string fixed to a wall. The sphere is pushed away from the wall by a stick. The forces acting on the sphere are shown in the second diagram. Which of the following statements is wrong?
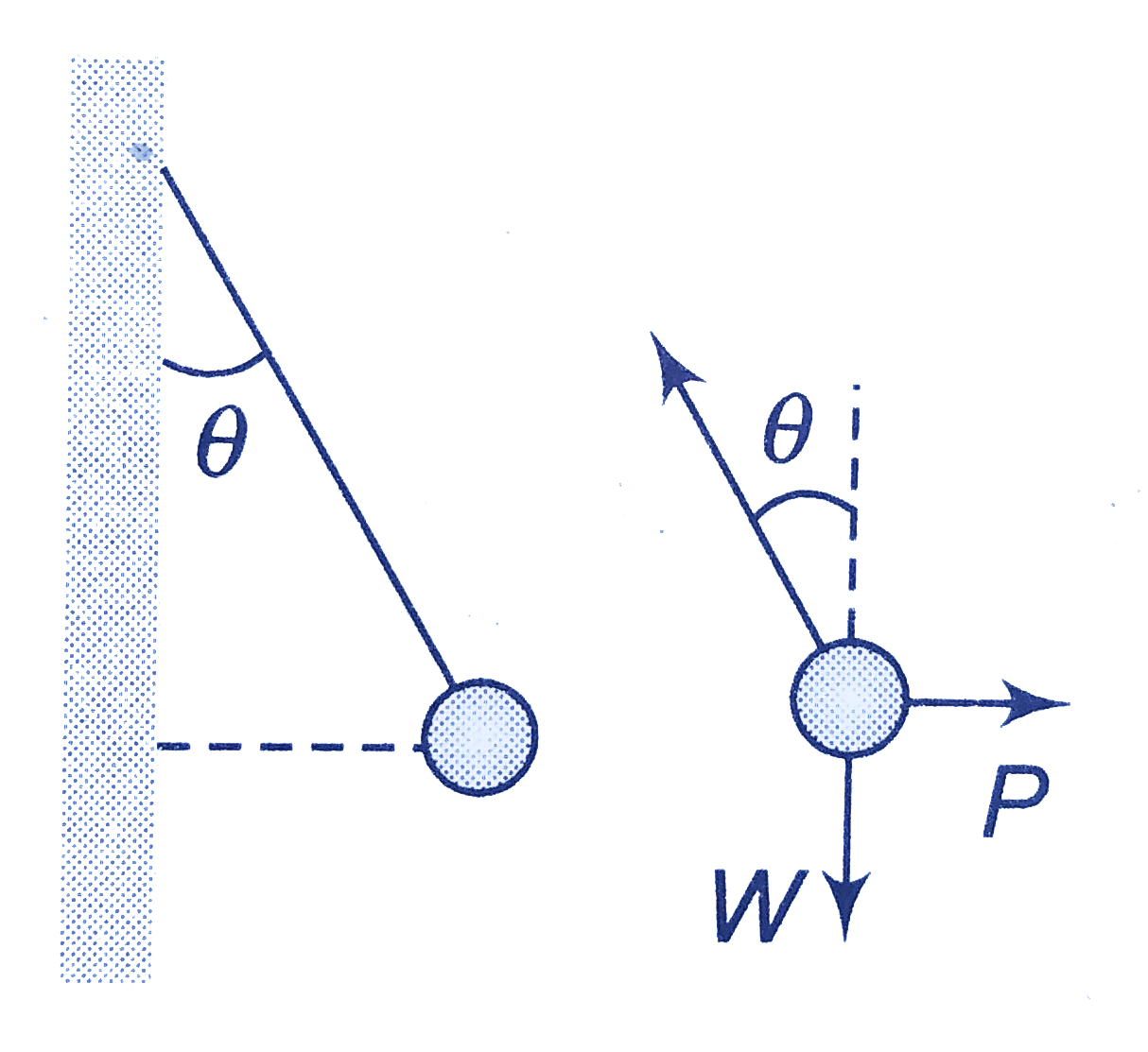 View Solution
View Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,View SolutionA plank with a uniform sphere placed on it resting on a smooth horizontal plane. Plank is pulled to right by a constant force F. If sphere does not slip over the plank. Which of the following is incorrect?
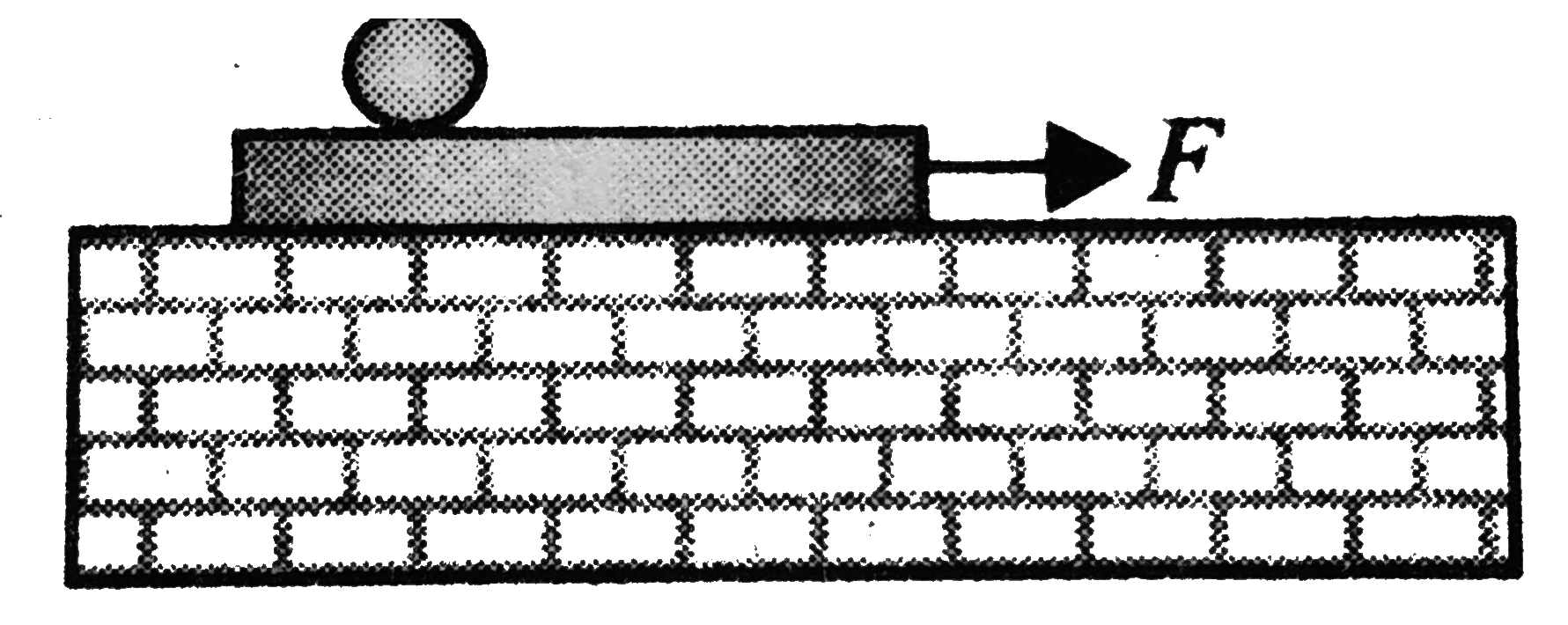 View Solution
View SolutionA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.
 View Solution
View Solution
