A ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
0≤v≤2u
v=u, if CP is horizontal
v=u, if CP makes an angle of 30∘ with the horizontal and P is below the horizontal level of C.
v=√2u, if CP is horizontal
The correct Answer is:A, C, D
To solve the problem, we need to analyze the motion of a ring rolling without slipping and determine the speed of a point P on the ring with respect to the ground. Let's break down the steps involved in finding the speed v of point P.
1. Understanding the Motion of the Ring:
- The ring rolls without slipping on the ground, meaning that the point of contact with the ground has zero velocity relative to the ground.
- The center of the ring C moves with a constant speed u.
2. Identifying the Speed Components:
- For any point P on the ring, the total velocity vP can be expressed as:
vP=vP,cm+vcm
where vP,cm is the velocity of point P relative to the center of mass C, and vcm is the velocity of the center of mass with respect to the ground, which is u.
3. Analyzing the Point of Contact:
- The point of contact between the ring and the ground has zero velocity. Therefore, if we consider the ring's rotation, the velocity of the point at the bottom (point of contact) is zero.
4. Calculating the Velocity of Point P:
- The speed of point P will depend on its position on the ring.
- If P is at the top of the ring, it will have both the translational speed of the center u and the tangential speed due to rotation ωr (where ω is the angular velocity and r is the radius of the ring). Since u=ωr, the total speed at the top will be:
vmax=u+u=2u
- If P is at the bottom (point of contact), the speed will be:
vmin=u−u=0
5. Considering Other Positions:
- For point P at a horizontal position (to the right or left of C), it will have a resultant speed of:
v=√u2+u2=u√2
- If point P makes an angle θ with the horizontal, we can resolve the velocities into components and use trigonometric relations to find the resultant speed.
6. Conclusion:
- The maximum speed v of point P can vary from 0 to 2u depending on its position on the ring. The specific values depend on the angle or position of point P relative to the center C.
- The ring rolls without slipping on the ground, meaning that the point of contact with the ground has zero velocity relative to the ground.
- The center of the ring C moves with a constant speed u.
- For any point P on the ring, the total velocity vP can be expressed as:
vP=vP,cm+vcm
where vP,cm is the velocity of point P relative to the center of mass C, and vcm is the velocity of the center of mass with respect to the ground, which is u.
- The point of contact between the ring and the ground has zero velocity. Therefore, if we consider the ring's rotation, the velocity of the point at the bottom (point of contact) is zero.
- The speed of point P will depend on its position on the ring.
- If P is at the top of the ring, it will have both the translational speed of the center u and the tangential speed due to rotation ωr (where ω is the angular velocity and r is the radius of the ring). Since u=ωr, the total speed at the top will be:
vmax=u+u=2u
- If P is at the bottom (point of contact), the speed will be:
vmin=u−u=0
- For point P at a horizontal position (to the right or left of C), it will have a resultant speed of:
v=√u2+u2=u√2
- If point P makes an angle θ with the horizontal, we can resolve the velocities into components and use trigonometric relations to find the resultant speed.
- The maximum speed v of point P can vary from 0 to 2u depending on its position on the ring. The specific values depend on the angle or position of point P relative to the center C.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is
 View Solution
View SolutionA wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed v0. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)
View SolutionA ring rolls without slipping on a horizontal surface. At any instant its position is as shown in the figure.
View SolutionConsider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
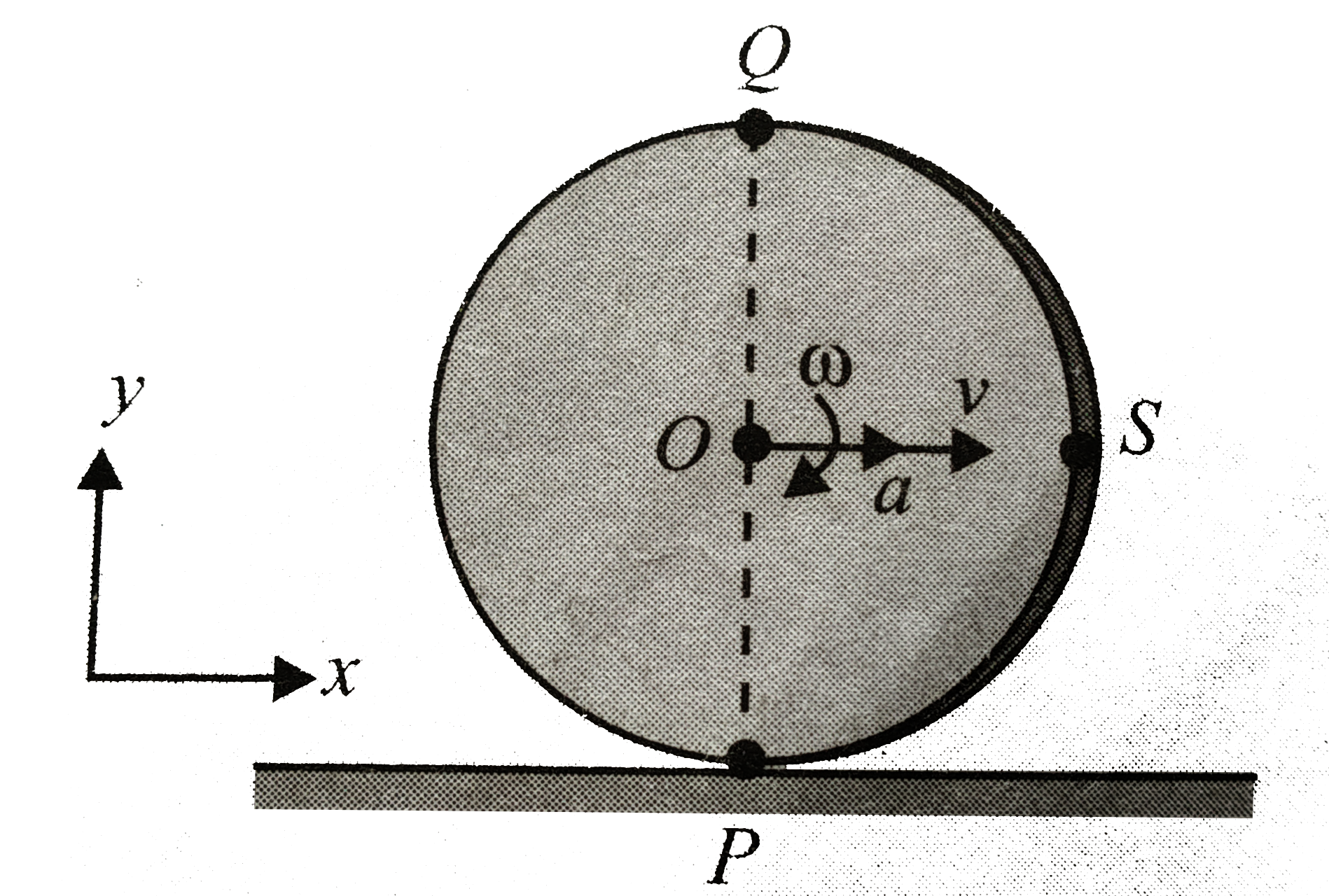 View Solution
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View Solution
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.View Solution
A uniform circular ring rolls without slipping on a horizontal surface. At any instant, its position is as shown in the figure. ThenView SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
View SolutionAssertion: A ring is rolling without slipping on a rough ground. It strikes elastically with a smooth wall as shown in figure. Ring will stop after some time while travelling in opposite direction.
Reason: After impact net angular momentum about an axis passing through bottommost point and perpendicular to plane of paper is zero.
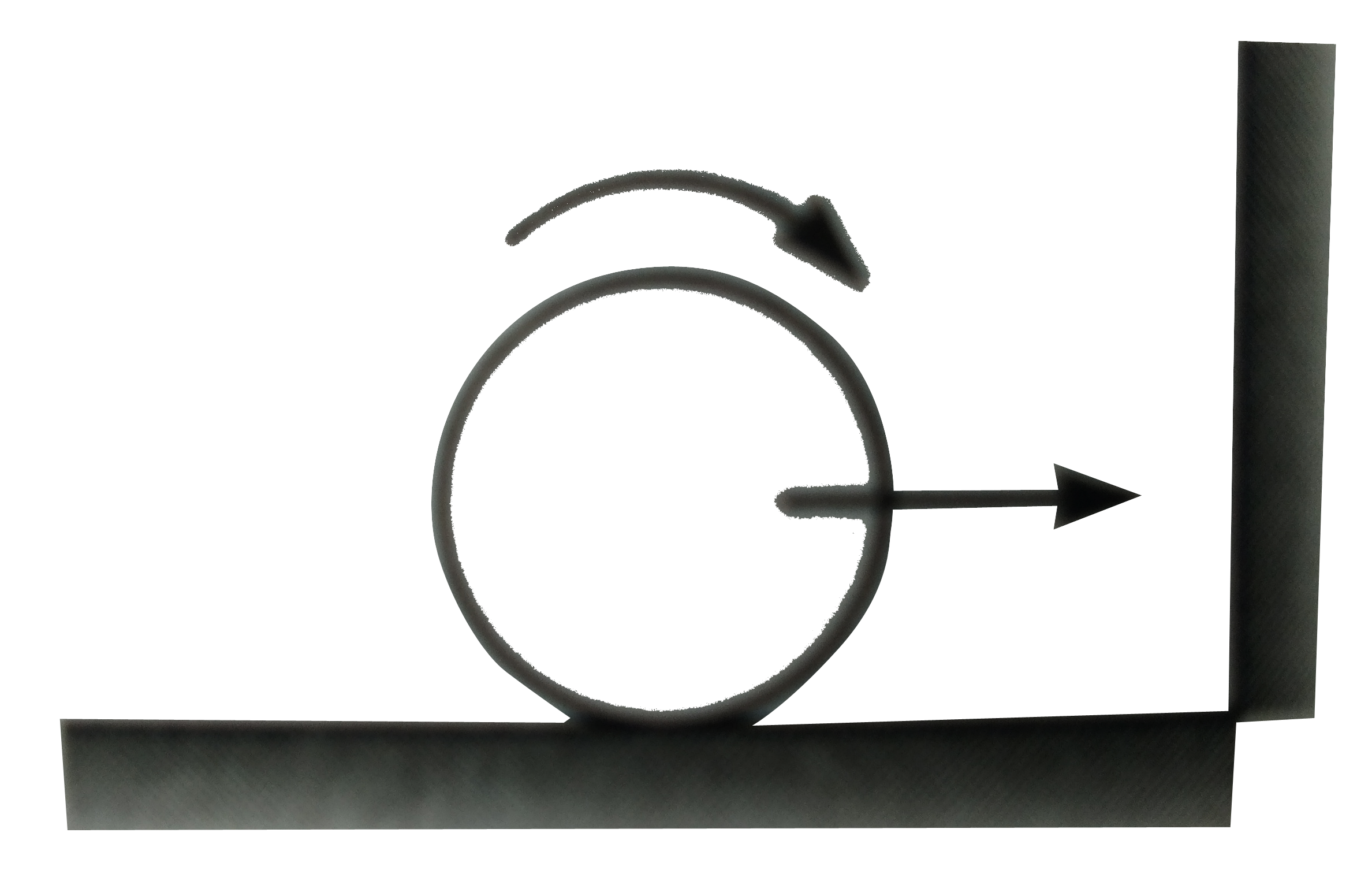 View Solution
View Solution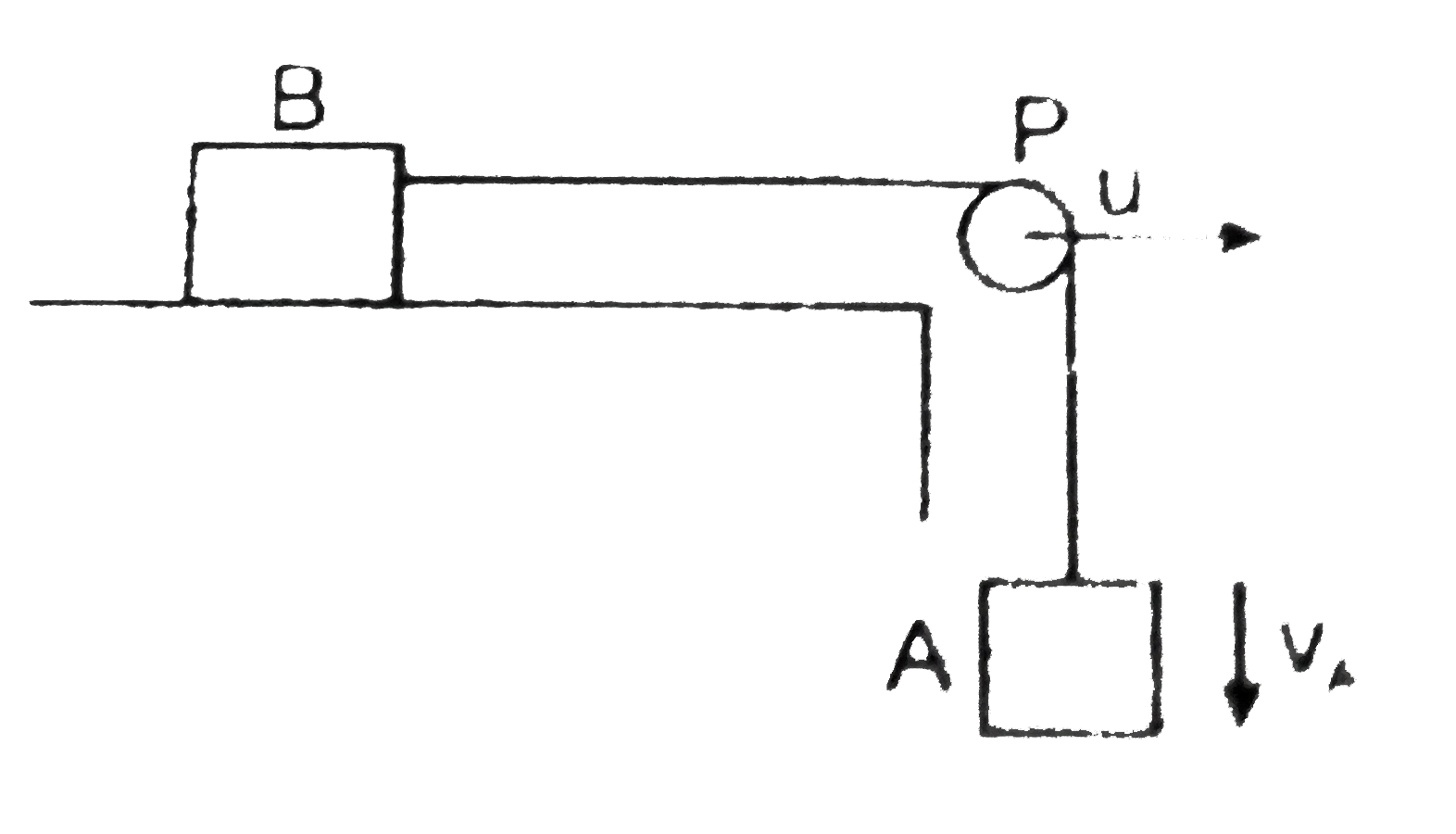
In the figure the pulley P moves to the right with a constant speed u. The downward speed of A is vA and the speed of B to the right VB.View Solution


