A 1.00mH inductor and a 1.00μF capacitor are connected in series. The current in the circuit is described by i=20t, where t, is in second and i is in ampere. The capacitor initially has no charge. Determine
(a) the voltage across the inductor as a function of time,
(b) the voltage across the capacitor as a function of time,
(c) the time when the energy stored in the capacitor first exceeds that in the inductor.
The correct Answer is:2×10−2V; b. 107t2V; c. 2√10×10−5s
I=20t

Vinductor=LdIdt=1×10−3×20=2×10−2V
b. Q=∫t0Idt⇒Q=10t2
Vcapacitor=QC=10t210−6=107t2V ltbr c. Energy in capacitor =12×C×V2
UC=12×10−6×1014t4=12×108t4
Uinductor=12×L×I2=12×1×10−3×400t2
=12×4×t210
Ucap=Uind
⇒=12×108×t4=12×410×t2
⇒t=2√10×10−5s
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
The current through an inductor of 1H is given by i=31sint. Find the voltage across the inductor.
View SolutionA charged capacitor and an inductor are connected in series at time t= 0. In terms of the period T of the resulting oscillations. determine how much later the following reach their maximum value: (a) the charge on the capacitor, (b) the voltage across the capacitor, with its original polarity: (c) the energy stored in the electric field, and (d) the current.
View Solution
Knowledge Check
Let q be the charge on the capacitor at any time t. The voltage V across the capacitor is
AVmsinωt=qCBVmcosωt=2VCCVmcosωt=q2CDVmsinωt=2qCThe circuit shown has been connected for a long time. The voltage across the capacitor is
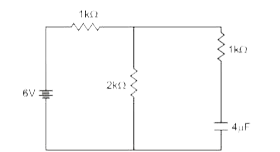 A1.2VB2.0 VC2.4VD4.0 V
A1.2VB2.0 VC2.4VD4.0 VA charged capacitor and an inductor are connected in series. At time t = 0, the current is zero, but the capacitor is charged. If T is the period of the resulting oscillations, the next time after t = 0, the maximum voltage across the inductor is
ATBT/4CT/2DT
The current in a 90mH inductor changes with time as i=1.0t2, where I is in amperes and t is in seconds.
View SolutionIn the circuit shown, the capacitor is initially uncharged. The switch S is closed at t = 0. Time after which voltage across capacitor and resistor are equal is:
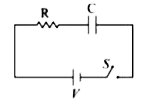
View SolutionIf the current through an inductor of 2 H is given by I=tsintA, then the voltage across the inductor is
View SolutionIn a series circuit C=2μF,L=1mH and R=10Ω, when the current in the circuit is maximum, at that time the ratio of the energies stored in the capacitor and the inductor will be
View SolutionIn series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View Solution
