a 100kg gun fires a ball of 1kg horizontally from a cliff of height 500m. If falls on the ground at a distance of 400m from the bottom of the cliff. The recoil velocity of the gun is (Take g: 10ms−2
0.2ms−1
0.4ms−1
0.6ms−1
0.8ms−1
The correct Answer is:B
To solve the problem of finding the recoil velocity of the gun when it fires a ball horizontally from a cliff, we can follow these steps:
Step 1: Identify the given data
- Mass of the gun, Mg=100kg
- Mass of the ball, Mb=1kg
- Height of the cliff, h=500m
- Horizontal distance from the base of the cliff where the ball lands, d=400m
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the time of flight of the ball
The time t it takes for the ball to fall from the height of the cliff can be calculated using the formula for free fall:
h=12gt2
Rearranging this gives:
t=√2hg
Substituting the values:
t=√2×50010=√100=10s
Step 3: Calculate the horizontal velocity of the ball
The horizontal distance d traveled by the ball can be expressed as:
d=u⋅t
Where u is the horizontal velocity of the ball. Rearranging gives:
u=dt
Substituting the values:
u=40010=40m/s
Step 4: Apply conservation of momentum
Since there are no external horizontal forces acting on the system, the momentum before firing must equal the momentum after firing. Before firing, the total momentum is zero. After firing:
Mb⋅u+Mg⋅vg=0
Where vg is the recoil velocity of the gun. Rearranging gives:
Mg⋅vg=−Mb⋅u
Thus,
vg=−Mb⋅uMg
Step 5: Substitute the known values to find vg
Substituting the values:
vg=−1⋅40100=−0.4m/s
Conclusion
The recoil velocity of the gun is −0.4m/s. The negative sign indicates that the direction of the recoil is opposite to the direction of the ball's motion.
- Mass of the gun, Mg=100kg
- Mass of the ball, Mb=1kg
- Height of the cliff, h=500m
- Horizontal distance from the base of the cliff where the ball lands, d=400m
- Acceleration due to gravity, g=10m/s2
The time t it takes for the ball to fall from the height of the cliff can be calculated using the formula for free fall:
h=12gt2
Rearranging this gives:
t=√2hg
Substituting the values:
t=√2×50010=√100=10s
The horizontal distance d traveled by the ball can be expressed as:
d=u⋅t
Where u is the horizontal velocity of the ball. Rearranging gives:
u=dt
Substituting the values:
u=40010=40m/s
Since there are no external horizontal forces acting on the system, the momentum before firing must equal the momentum after firing. Before firing, the total momentum is zero. After firing:
Mb⋅u+Mg⋅vg=0
Where vg is the recoil velocity of the gun. Rearranging gives:
Mg⋅vg=−Mb⋅u
Thus,
vg=−Mb⋅uMg
Substituting the values:
vg=−1⋅40100=−0.4m/s
The recoil velocity of the gun is −0.4m/s. The negative sign indicates that the direction of the recoil is opposite to the direction of the ball's motion.
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:HOTS
Explore 8 Videos
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:Exemplar Problems
Explore 9 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
Similar Questions
A drop of mass 2.0 g falls from a cliff of height 1.0 km It hits the ground with a speed of 50.0ms−1. The work done by the resistive force is
View SolutionA bullet of mass 5 g is fired at a velocity of 900ms−1 from a rifle of mass 2.5 kg. What is the recoil velocity of the rifle?
View SolutionA ball is thrown horizontally from a cliff such that it strikes the ground after 5s.The line of sight makes an angle 37∘ with the horizontal.The initial velocity of projection in ms−1 is
View SolutionA gun of mass M. fires a shell of mass m horizontally and the energy of explosion is such as would be sufficient to project the shell vertically to a height 'h' . The recoil velocity of the gun is
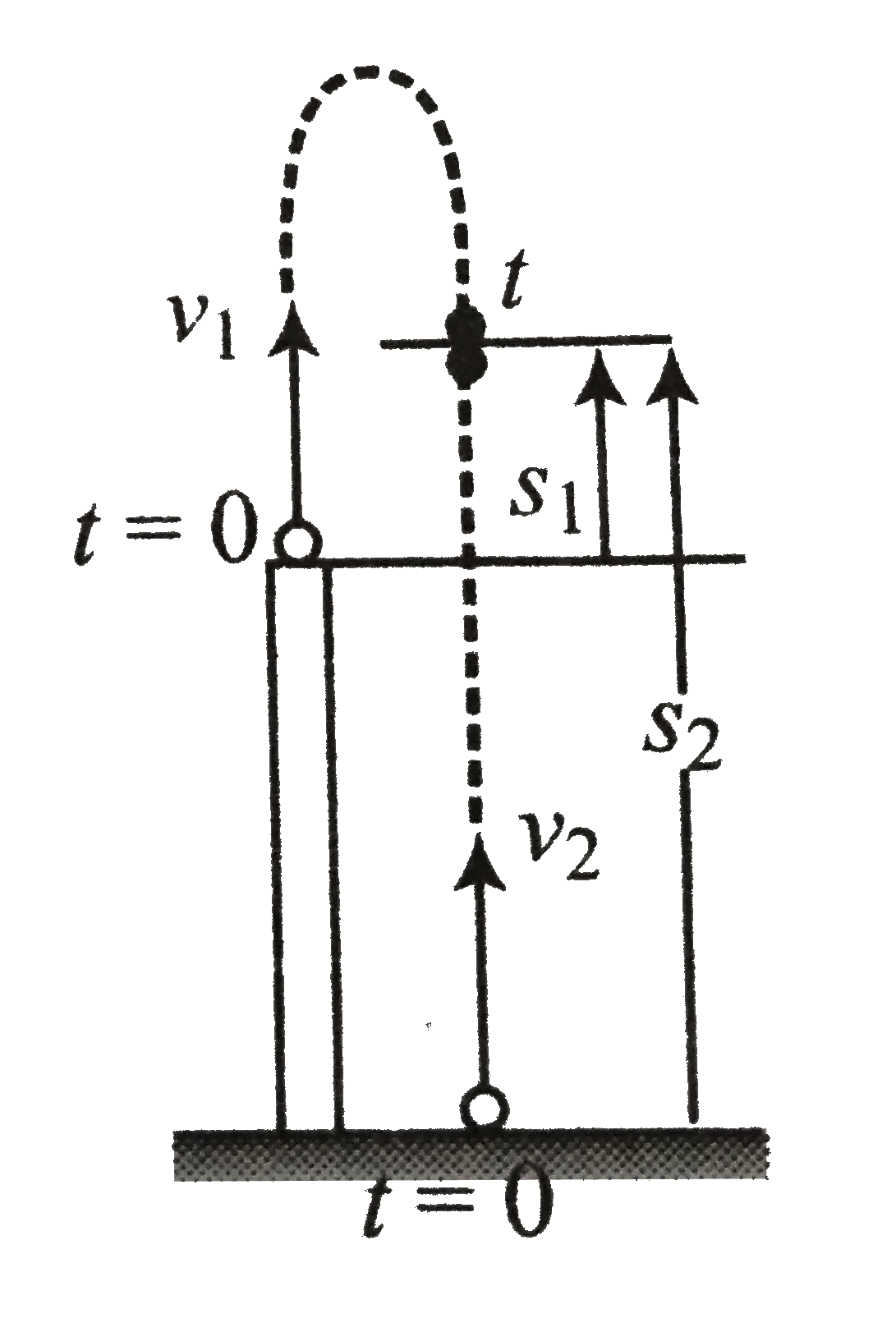
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10m and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
View SolutionA body of mass m=2kg falls from a height h=10m from the ground level .
What is the magnitude of total change in momentum of the body before it strikes the ground?
View SolutionA bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s. If mass of the gun is 4 kg, then calculate the recoil velocity of the gun.
View SolutionA bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s . If mass of the gun is 4 kg , then calculate the recoil velocity of the gun .
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA bullet of mass 40 g is fired from a gun of mass 10 kg. If velocity of bullet is 400 m/s. then the recoil velocity of the gun wil be
View Solution