A 2.00 kg particle moves along an x axis in onedimensional motion while a conservative force along that axis acts on it. The potential energy U(x) associated with the force is plotted in Fig. 8-36a. That is, if the particle were placed at any position between x=0 and x=7.00m, it would have the plotted value of U. At x=6.5m, the particle has velocity →v0=(−4.00m/s)ˆi.
(a) Form Fig. 8-36a, determine the particle's speed at x1=4.5m.
KEY IDEA
(1) The particle.s kinetic energy is given by Eq. 8-1 (K=1/2mv2). (2) Because only a conservative force acts on the particle, the mechanical energy Emec(=K+U) is conserved as the particle moves. (3) Therefore, on a plot of U(x) such as Fig. 8-36a, the kinetic energy is equal to the difference between Emec and U.
Calculations: At x=6.5m, the particle has kinetic energy
K0=12mv20=12(2.00kg)(4.00m/s)2
=16.0J.
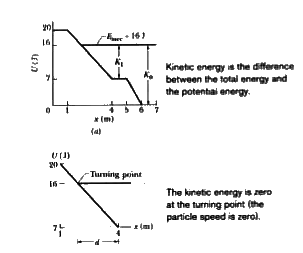
Figure 8-36 (a) A plot of potential energy U versus position x.
(b) A section of the plot used to find where the particle turns around.
Because the potential energy there is U=0, the mechanical energy is
Emec=K0+U0+16.0J+0=16.0J.
This value for Emec is plotted as a horizontal line in Fig. 8-36 a. From that figure we see that at x=4.5m, the potential energy is U1=7.0J. The kinetic energy K1 is the difference between Emec and U1:
K1=Emec−U1=16.0J−7.0J=9.0J.
Because K1=1/2mv21, we
v1=3.0m/s.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:CHECKPOINT
Explore 6 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PROBLEMS
Explore 58 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Integer Type)
Explore 4 Videos
Similar Questions
A 2.00 kg particle moves along an x axis in onedimensional motion while a conservative force along that axis acts on it. The potential energy U(x) associated with the force is plotted in Fig. 8-36a. That is, if the particle were placed at any position between x=0 and x=7.00m, it would have the plotted value of U. At x=6.5m, the particle has velocity →v0=(−4.00m/s)ˆi.
(b) Where is the particle's turning point located?
View SolutionA 2.00 kg particle moves along an x axis in onedimensional motion while a conservative force along that axis acts on it. The potential energy U(x) associated with the force is plotted in Fig. 8-36a. That is, if the particle were placed at any position between x=0 and x=7.00m, it would have the plotted value of U. At x=6.5m, the particle has velocity →v0=(−4.00m/s)ˆi.
(c) Evaluate the force acting on the particle when it is in the region 1.9 m<x<4.0 m.
View Solution
Knowledge Check
A particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
ADuring the course of its motion the maximum speed of the particle will be √43m/sBParticle will never cross the origin.CParticle will come to its equilibrium position for the first time at 5π4√3 secondDThe amplitude of oscillationi for the particle is 1mA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum and minimum values of x, respectively, areA7.38m,−3.38mB6.38m,−4.38mC7.38m,−2.83mD6.38m,−2.38mA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
What is the mechanical energy of a system?A(a) 35JB(b) 64JC(c) 86JD(d) 49J
A particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
What is the mechanical energy of a system?
View SolutionThe potential energy of a particle in motion along X axis is given by U=U0−u0 cos ax. The time period of small oscillation is
View SolutionA conservative force acts on a 4 kg particle in x direction. The potential energy U(x) is given by U(X)=40+(x–6)2, where x is in metre. If it is given that at x = 8 m, KE is 30 J then find the maximum KE of the particle.
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View Solution
