A 2.00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
The correct Answer is:A, B, C
To solve the problem, we will follow these steps:
Given Data:
- Length of the rope (L) = 2.00 m
- Mass of the rope (m) = 80 g = 0.08 kg
- Tension in the string (T) = 256 N
Step 1: Calculate the mass per unit length (μ)
The mass per unit length (μ) is given by the formula:
μ=mL
Substituting the values:
μ=0.08kg2.00m=0.04kg/m
Step 2: Calculate the wave velocity (v)
The velocity of the wave on the string is given by:
v=√Tμ
Substituting the values:
v=√256N0.04kg/m=√6400=80m/s
Step 3: Determine the frequencies of the fundamental and the first two overtones
For a string fixed at one end, the frequencies are given by:
fn=(2n+1)v4L
Where n is the harmonic number (0 for fundamental, 1 for first overtone, 2 for second overtone).
Fundamental Frequency (n = 0):
f0=(2⋅0+1)⋅80m/s4⋅2.00m=808=10Hz
First Overtone (n = 1):
f1=(2⋅1+1)⋅80m/s4⋅2.00m=3⋅808=30Hz
Second Overtone (n = 2):
f2=(2⋅2+1)⋅80m/s4⋅2.00m=5⋅808=50Hz
Step 4: Calculate the wavelengths for the fundamental and the first two overtones
The wavelength for each mode is given by:
λn=4L2n+1
Wavelength for Fundamental (n = 0):
λ0=4⋅2.00m2⋅0+1=81=8m
Wavelength for First Overtone (n = 1):
λ1=4⋅2.00m2⋅1+1=83≈2.67m
Wavelength for Second Overtone (n = 2):
λ2=4⋅2.00m2⋅2+1=85=1.6m
Final Results:
- Frequencies:
- Fundamental Frequency: f0=10Hz
- First Overtone: f1=30Hz
- Second Overtone: f2=50Hz
- Wavelengths:
- Wavelength for Fundamental: λ0=8m
- Wavelength for First Overtone: λ1≈2.67m
- Wavelength for Second Overtone: λ2=1.6m
- Length of the rope (L) = 2.00 m
- Mass of the rope (m) = 80 g = 0.08 kg
- Tension in the string (T) = 256 N
The mass per unit length (μ) is given by the formula:
μ=mL
Substituting the values:
μ=0.08kg2.00m=0.04kg/m
The velocity of the wave on the string is given by:
v=√Tμ
Substituting the values:
v=√256N0.04kg/m=√6400=80m/s
For a string fixed at one end, the frequencies are given by:
fn=(2n+1)v4L
Where n is the harmonic number (0 for fundamental, 1 for first overtone, 2 for second overtone).
f0=(2⋅0+1)⋅80m/s4⋅2.00m=808=10Hz
f1=(2⋅1+1)⋅80m/s4⋅2.00m=3⋅808=30Hz
f2=(2⋅2+1)⋅80m/s4⋅2.00m=5⋅808=50Hz
The wavelength for each mode is given by:
λn=4L2n+1
λ0=4⋅2.00m2⋅0+1=81=8m
λ1=4⋅2.00m2⋅1+1=83≈2.67m
λ2=4⋅2.00m2⋅2+1=85=1.6m
- Frequencies:
- Fundamental Frequency: f0=10Hz
- First Overtone: f1=30Hz
- Second Overtone: f2=50Hz
- Wavelength for Fundamental: λ0=8m
- Wavelength for First Overtone: λ1≈2.67m
- Wavelength for Second Overtone: λ2=1.6m
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -29videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
Similar Questions
A 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionA 160 g rope 4 m long is fixed at one end and tied to a light string of the same length at the other end. Its tension is 400 N.
(a) What are the wavelength of the fundamental and the first two overtones?
(b) What are the frequencies of these standing waves?
[Hint : In this case, fixed end is a node and the end tied with the light string is antinode.]View SolutionA steel wire of mass 4.0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
View SolutionA 20cm long string, having a mass of 1.0g, is fixed at both the ends. The tension in the string is 0.5N. The string is into vibrations using an external vibrator of frequency 100Hz. Find the separation (in cm) between the successive nodes on the string.
View SolutionA string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
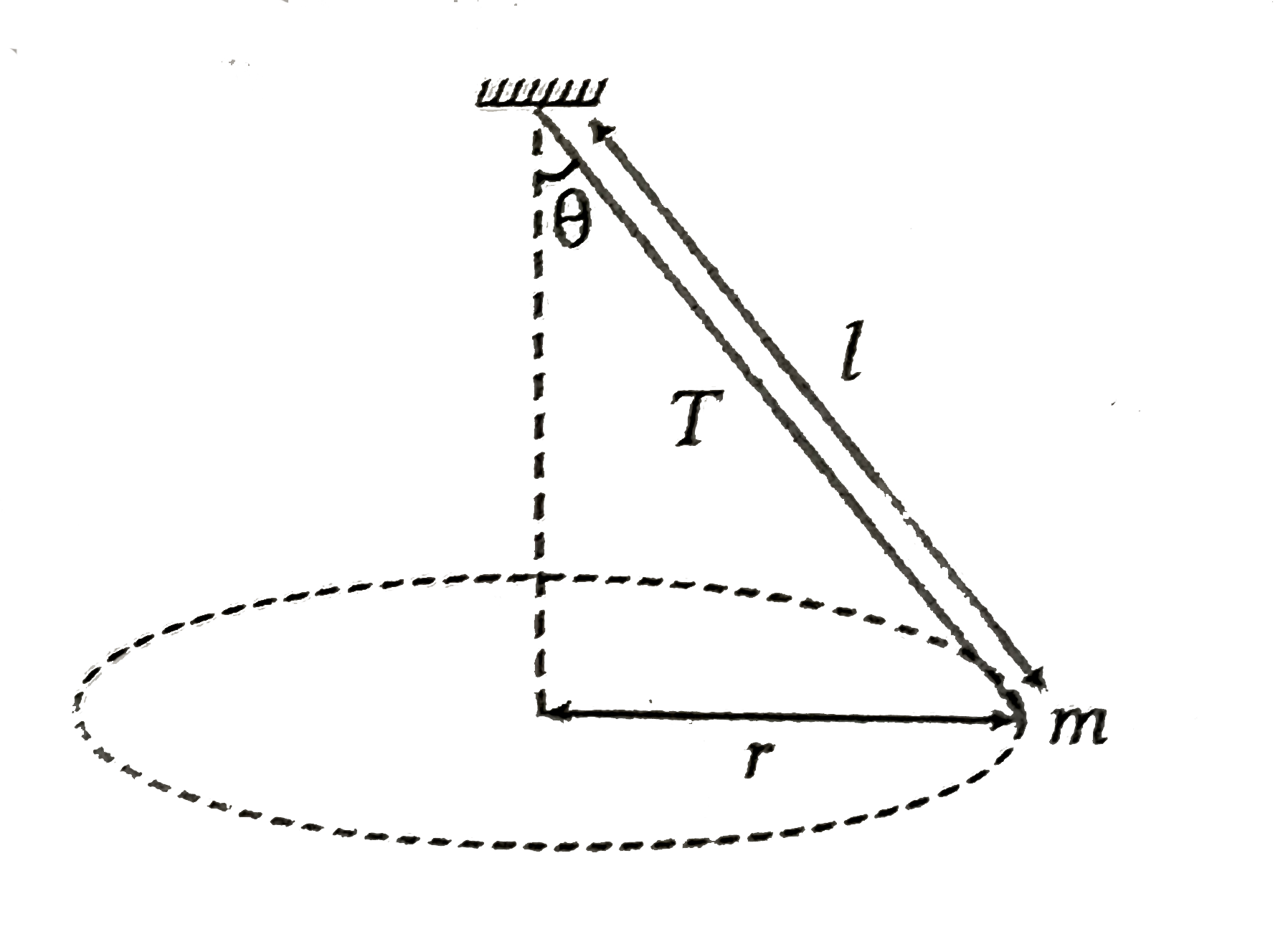 View Solution
View SolutionA 2 m-long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m s and the amplitude is 0.5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x= 50 cm has reached its maximum displacement.
View SolutionA wire of length 1m and mass 20g is stretched with a force of 800 N. Find the fundamental frequency. Also find the frequencies of the first two Overtones.
View SolutionA string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/s, find the tension in the string.
View SolutionA string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/s, find the tension in the string.
View SolutionA 1.50 m long rope is stretched between two supports with a tension that makes the speed of transverse waves 48.0m/s. What are the wavelength and frequency of
(a) the fundamental?
(b) the second overtone?
(c) the fourth harmonic?View Solution

