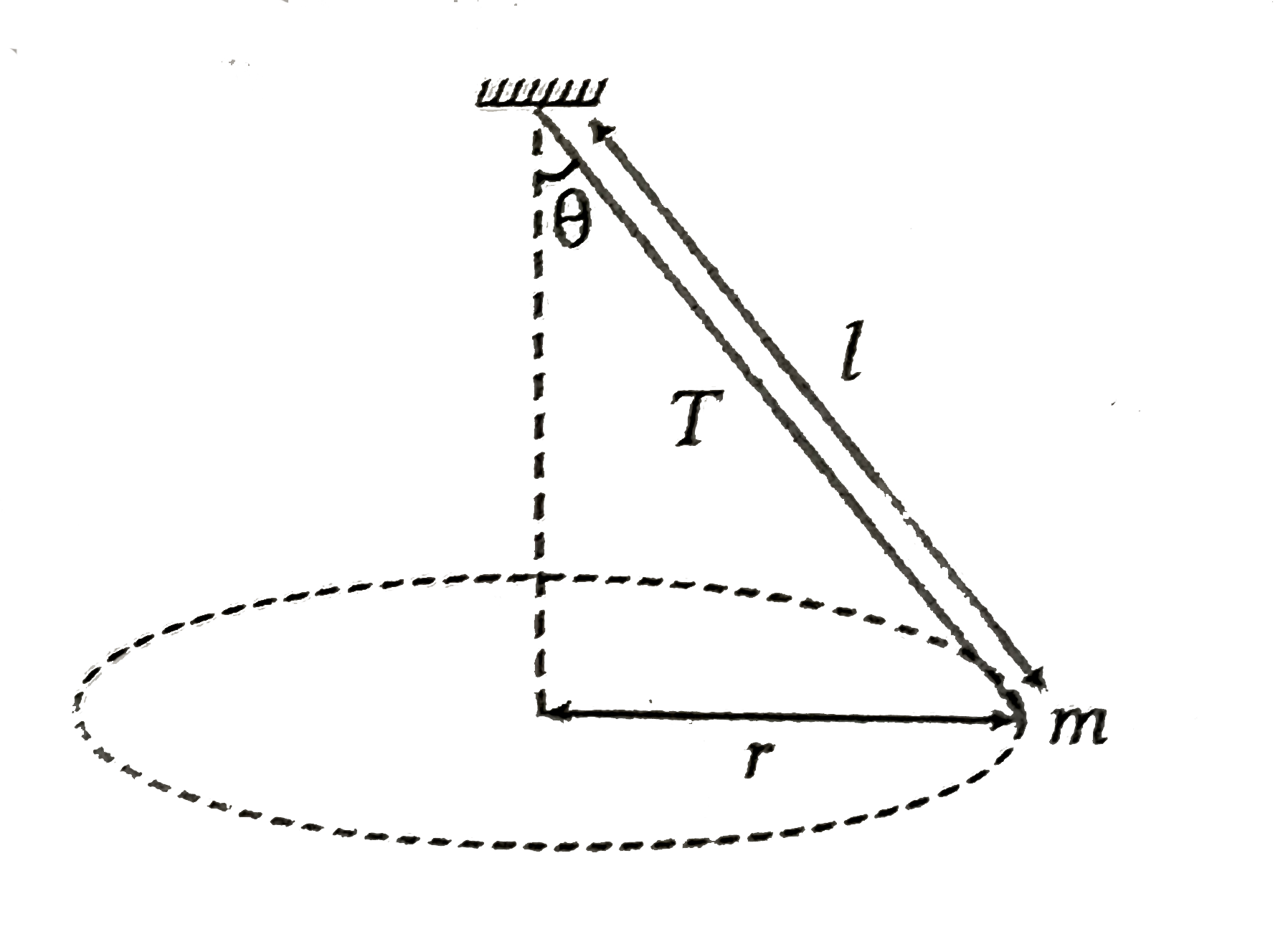
A string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
16 ml
4 ml
8 ml
2 ml
The correct Answer is:A
Balancing horizontal forces,
Tsinθ=mrω2
or Tsinθ=m(lsinθ)ω2
∴ T=mlω2=ml(2πf)2
=ml(2π×2π)2=16ml
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns3videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point45videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
In a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100 g and the string makes 2πmvs−1around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
View SolutionIn a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100 g and the string makes 2 π r v s − 1 around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g = 10 m s − 1 )
View Solution
Knowledge Check
- Question 1 - Select One
One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
Ay(t)=Asin(2πx)6cos(50πt)3By(t)=Asin(πx)3cos(100πt)3Cy(t)=Asin(5πx)6cos(255πt)3Dy(t)=Asin(5πx)2cos250πt
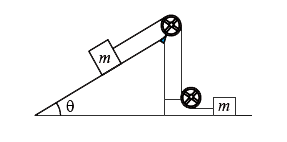
Two blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
 View Solution
View SolutionA massless string passes over a frictionless pulley and carries mass m1 hanging at one end and mass m2 connected by another massless string to mass m3 at other end as shown in figure. Calculate the tension in string joining masses m2andm3.
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves with an amplitude of 1.12 cm . The motion of the bar is continuous and is repeated regularly 120 times per second. The string has linear density of 117g/m. The other end of the string is attached to a mass 4.68 kg. The string passes over a smooth pulley and the mass attached to the other end of the string hangs freely under gravity.
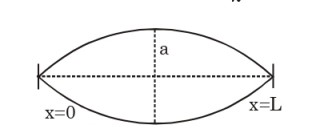
The maximum magnitude of the transverse component of tension in the string isView SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).
 View Solution
View SolutionA 2.00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution

