A 3 m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in the following figure, Find the reaction forces of the wall and the floor.

Video Solution

Text Solution

Verified by Experts

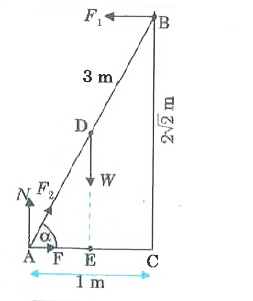
Here, AB=3m
AC=1m
$B C = \sqrt{A B^{2} - A C^{2}} = \sqrt{3^{2} - 1^{2}} = 2 \sqrt{2} m$
Force acting on the ladder:
1. Weight acting at centre of gravity D
2. Reaction force $F_{1}$ of the wall at B
3. Reaction force $F_{2}$ of the floor at A, which can be resolved into two components: normal reaction N and force of friction F. The frictional force F prevents the ladder from sliding away from the wall and is thus directed towards the wall.
For translational equilibrium in vertical direction,
N=W
For translational equilibrium in horizontal direction,
$F = F_{1}$
For rotational equilibrium, considering the moments about point A, we have
$F_{1} \times B C = W \times A E [N, F_{2}$ and F will have zero moment about A]
$\Rightarrow F_{1} \times 2 \sqrt{2} = W \times \frac{1}{2}$
Given, $W = 20 g = 20 \times 9.8 = 196 N$
$∴ F_{1} = \frac{196}{4 \sqrt{2}} = 34.6 N$
N=W =196 N
$F = F_{1} = 34.6 N$
$F_{2} = \sqrt{{(F)}^{2} + N^{2}} = \sqrt{{34.6}^{2} + 196^{2}} = 199 N$
If $F_{2}$ makes and angle $α$ with F then
$tan α = \frac{N}{F} = 4 \sqrt{2} = 5.657$
$\Rightarrow α ≅ 80$

Updated on:21/07/2023

The height of the hall is 13 m and the perimeter of its floor is 430 m. Find the area of four walls of the hall.
A9590 $m^{2}$
B5590 $m^{2}$
C9055 $m^{2}$
D5059 $m^{2}$
A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is

A50N
B $50 \sqrt{3} N$
C $\frac{60}{\sqrt{3}} N$
D100N