A 4kg particle is moving along the x- axis under the action of the force F=−(π216)xN At t=2sec the particle passes through the origin and t=10sec, the speed is 4√2m/s The amplitude of the motion is
32√2πm
16πm
4πm
16√2πm
The correct Answer is:A
To solve the problem step by step, we will analyze the given force, relate it to simple harmonic motion, and find the amplitude of the motion.
Step 1: Identify the force and relate it to simple harmonic motion
The force acting on the particle is given by:
F=−π216x
This is in the form of Hooke's law, F=−kx, where k=π216. In simple harmonic motion, we have:
F=md2xdt2
Thus, we can equate:
mω2=k
where ω is the angular frequency.
Step 2: Calculate the angular frequency ω
Given the mass m=4kg:
ω2=km=π2164=π264
Taking the square root to find ω:
ω=π8rad/s
Step 3: Write the equation of motion
The general solution for the position x in simple harmonic motion is:
x(t)=Asin(ωt+ϕ)
where A is the amplitude and ϕ is the phase constant.
Step 4: Use the initial condition at t=2s
At t=2s, the particle passes through the origin, so:
x(2)=Asin(π8⋅2+ϕ)=0
This implies:
sin(π4+ϕ)=0
Thus:
π4+ϕ=nπfor some integer n
Choosing n=0:
ϕ=−π4
Step 5: Write the position equation with the phase constant
Now substituting ϕ back into the equation:
x(t)=Asin(π8t−π4)
Step 6: Use the condition at t=10s to find the amplitude
The speed v(t) is given by the derivative of x(t):
v(t)=dxdt=Aωcos(π8t−π4)
At t=10s, the speed is given as 4√2:
4√2=A⋅π8cos(π8⋅10−π4)
Calculating the argument:
π8⋅10−π4=5π4−2π4=3π4
Thus:
cos(3π4)=−1√2
Substituting back:
4√2=A⋅π8(−1√2)
Rearranging gives:
A=4√2⋅8−π/√2=−32π
Taking the absolute value (since amplitude is positive):
A=32π
Final Answer
The amplitude of the motion is:
A=32πm
The force acting on the particle is given by:
F=−π216x
F=md2xdt2
Thus, we can equate:
mω2=k
where ω is the angular frequency.
Given the mass m=4kg:
ω2=km=π2164=π264
Taking the square root to find ω:
ω=π8rad/s
The general solution for the position x in simple harmonic motion is:
x(t)=Asin(ωt+ϕ)
where A is the amplitude and ϕ is the phase constant.
At t=2s, the particle passes through the origin, so:
x(2)=Asin(π8⋅2+ϕ)=0
This implies:
sin(π4+ϕ)=0
Thus:
π4+ϕ=nπfor some integer n
Choosing n=0:
ϕ=−π4
Now substituting ϕ back into the equation:
x(t)=Asin(π8t−π4)
The speed v(t) is given by the derivative of x(t):
v(t)=dxdt=Aωcos(π8t−π4)
At t=10s, the speed is given as 4√2:
4√2=A⋅π8cos(π8⋅10−π4)
Calculating the argument:
π8⋅10−π4=5π4−2π4=3π4
Thus:
cos(3π4)=−1√2
Substituting back:
4√2=A⋅π8(−1√2)
Rearranging gives:
A=4√2⋅8−π/√2=−32π
Taking the absolute value (since amplitude is positive):
A=32π
The amplitude of the motion is:
A=32πm
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Spring Particle System24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm25videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle moves along x -axis under the action of a position dependent force F =(5x2−2x)N. Work done by forces on the particle when it moves from origin to x=3m is
A45JB36JC32JD42J - Question 2 - Select One
A particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
A45 JB36 JC32 JD42 J - Question 3 - Select One
A particle moves along the X-axis according to to the law S=asin2(ωt−π/4)
The amplitude of the oscillation isAaBa2C3a2D2a
A particle moving along the x axis has a position given by x=54t−2.0t3m. At the time t=3.0s, the speed of the particle is zero. Which statement is correct ?
View SolutionA particle moves along x-axis as x=4(t−2)+a(t−2)2
Which of the following is true?View Solutionvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
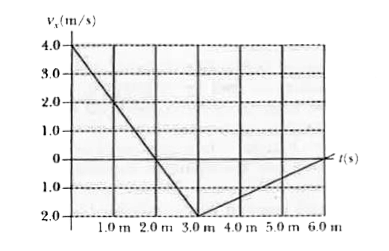 View Solution
View SolutionThe position of a particle moving on a stringht line under rthe action of a force is given as x=50t−5t2 Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is.
View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View Solution

