A 4μF capacitor, a resistance of 2.5MΩ is in series with 12V battery. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [ Given In (2) = 0.693]
13.86 s
6.93 s
7 s
14 s
The correct Answer is:A
To solve the problem, we need to find the time t after which the potential difference across the capacitor VC is three times the potential difference across the resistor VR in a circuit consisting of a capacitor, a resistor, and a battery.
1. Identify the given values:
- Capacitance, C=4μF=4×10−6F
- Resistance, R=2.5MΩ=2.5×106Ω
- Voltage of the battery, E=12V
2. Understand the relationships:
- The potential difference across the capacitor is given by:
VC=QC
- The potential difference across the resistor is given by:
VR=I⋅R
- The current I in a charging capacitor circuit is given by:
I=E−VCR
3. Set up the equation for the relationship between VC and VR:
- We need to find the time t when:
VC=3VR
- Substituting the expressions for VC and VR:
QC=3(E−VCR)R
- Rearranging gives:
Q=3(E−VC)C
4. Use the charging equation for the capacitor:
- The charge Q on the capacitor at time t is:
Q=C⋅E(1−e−tτ)
- Where τ=R⋅C is the time constant.
5. Substituting Q into the equation:
- Substitute Q into the equation:
C⋅E(1−e−tτ)=3(E−QC)C
- This simplifies to:
1−e−tτ=3(1−e−tτ)
6. Rearranging the equation:
- Rearranging gives:
4e−tτ=1
- Taking the natural logarithm of both sides:
−tτ=ln(0.25)=−2ln(2)
- Therefore:
t=2τln(2)
7. Calculate τ:
- Calculate τ:
τ=R⋅C=(2.5×106)⋅(4×10−6)=10
8. Final calculation of time t:
- Substitute τ into the equation for t:
t=2⋅10⋅0.693=13.86seconds
Final Answer:
The time after which the potential difference across the capacitor is three times the potential difference across the resistor is approximately 13.86 seconds.
- Capacitance, C=4μF=4×10−6F
- Resistance, R=2.5MΩ=2.5×106Ω
- Voltage of the battery, E=12V
- The potential difference across the capacitor is given by:
VC=QC
- The potential difference across the resistor is given by:
VR=I⋅R
- The current I in a charging capacitor circuit is given by:
I=E−VCR
- We need to find the time t when:
VC=3VR
- Substituting the expressions for VC and VR:
QC=3(E−VCR)R
- Rearranging gives:
Q=3(E−VC)C
- The charge Q on the capacitor at time t is:
Q=C⋅E(1−e−tτ)
- Where τ=R⋅C is the time constant.
- Substitute Q into the equation:
C⋅E(1−e−tτ)=3(E−QC)C
- This simplifies to:
1−e−tτ=3(1−e−tτ)
- Rearranging gives:
4e−tτ=1
- Taking the natural logarithm of both sides:
−tτ=ln(0.25)=−2ln(2)
- Therefore:
t=2τln(2)
- Calculate τ:
τ=R⋅C=(2.5×106)⋅(4×10−6)=10
- Substitute τ into the equation for t:
t=2⋅10⋅0.693=13.86seconds
The time after which the potential difference across the capacitor is three times the potential difference across the resistor is approximately 13.86 seconds.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
given that potential differene across 1μF capacitor is 10V. Then,
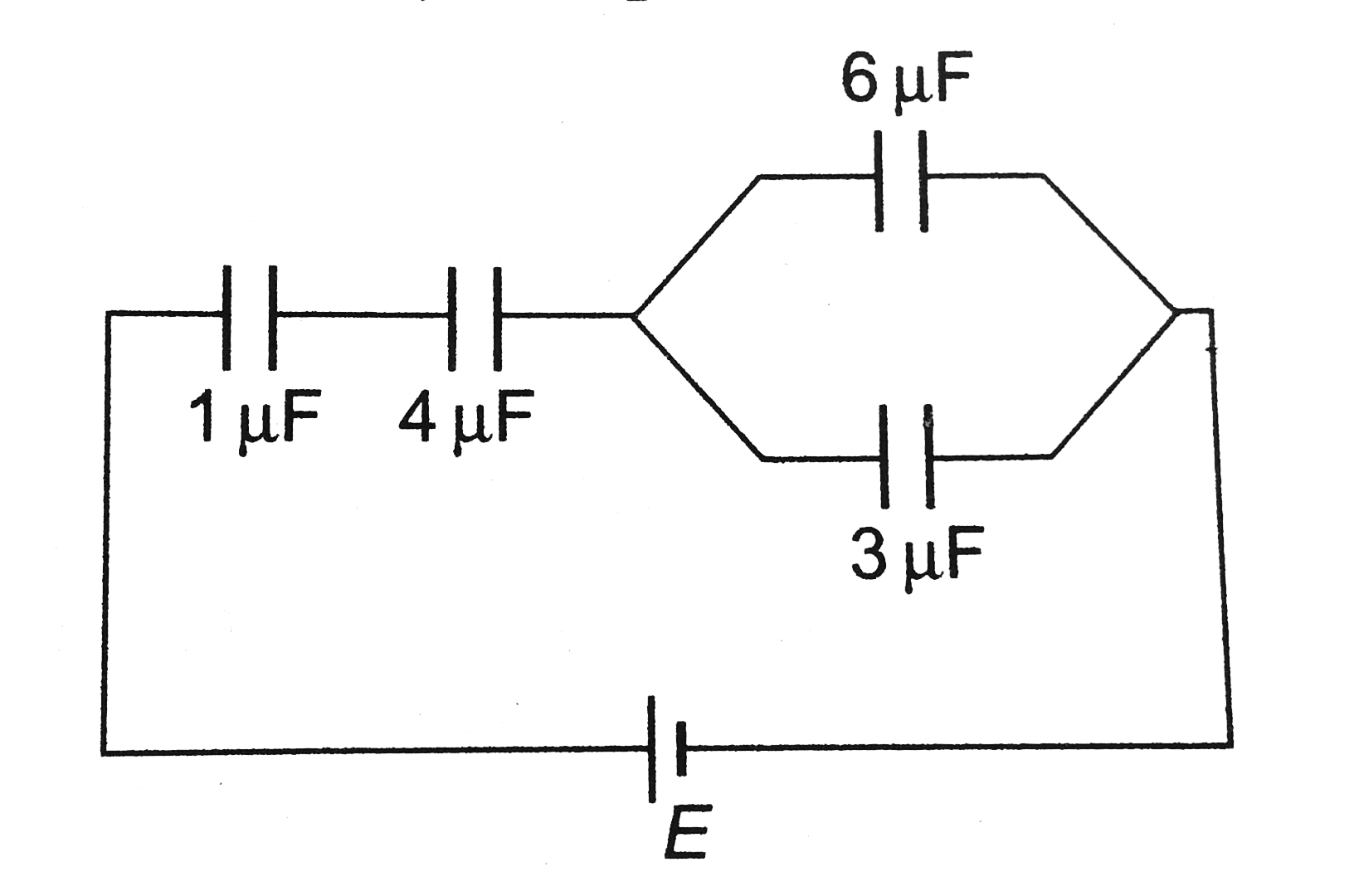
View SolutionIn the adjoning figure, the potential difference across the 4.5μF capacitor is

View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
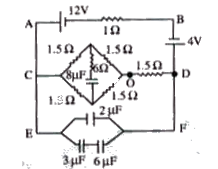
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
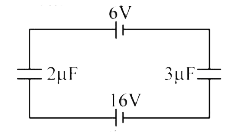
View SolutionFind charge on each capacitor and potential difference across each capacitor .

View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
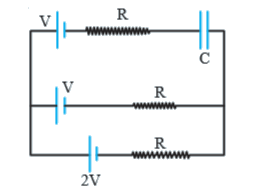
View SolutionFind potential difference across the resistance 300Ω in A and B.
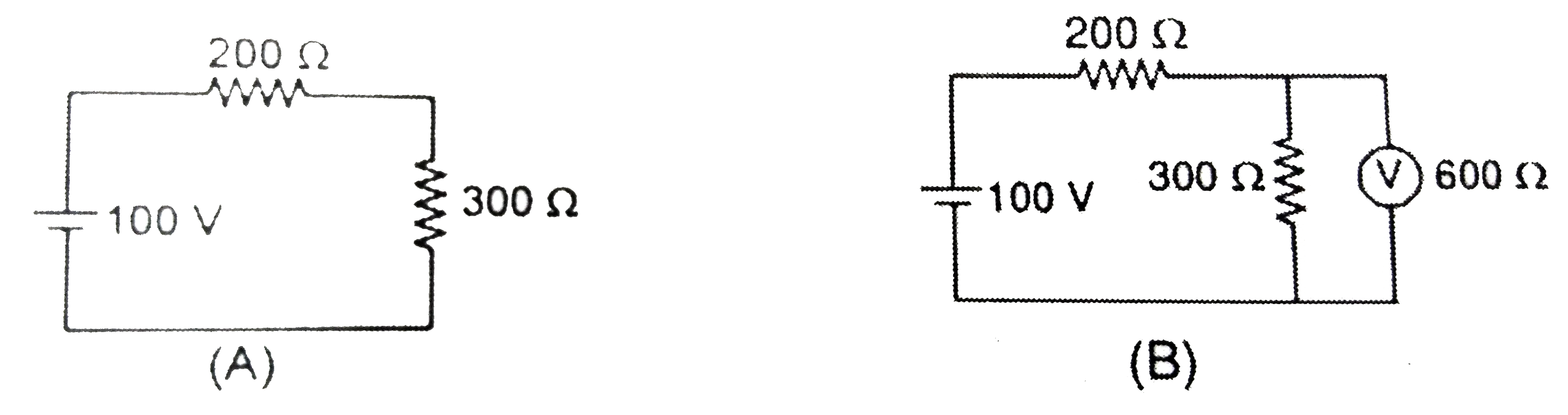
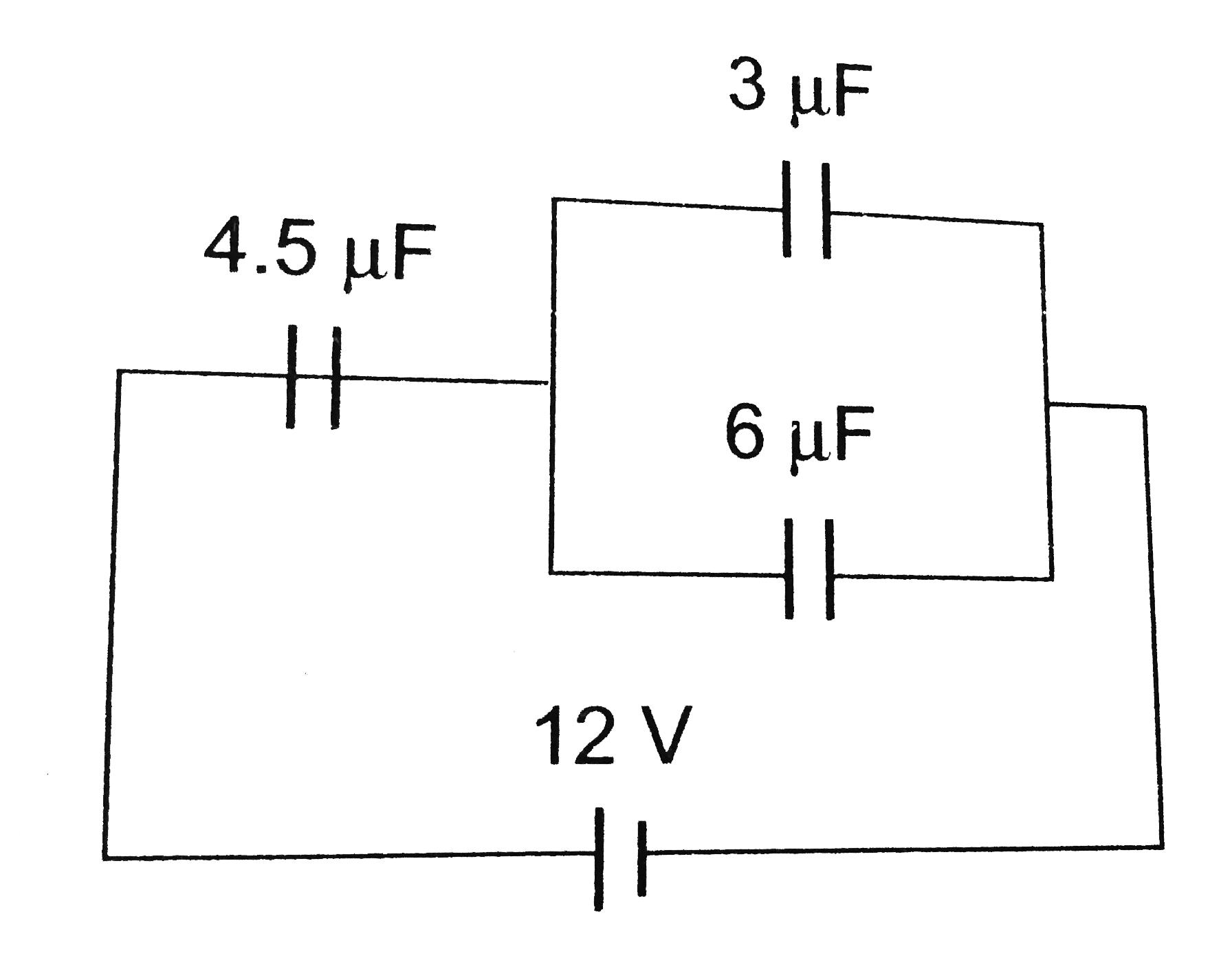
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.
View SolutionIf power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
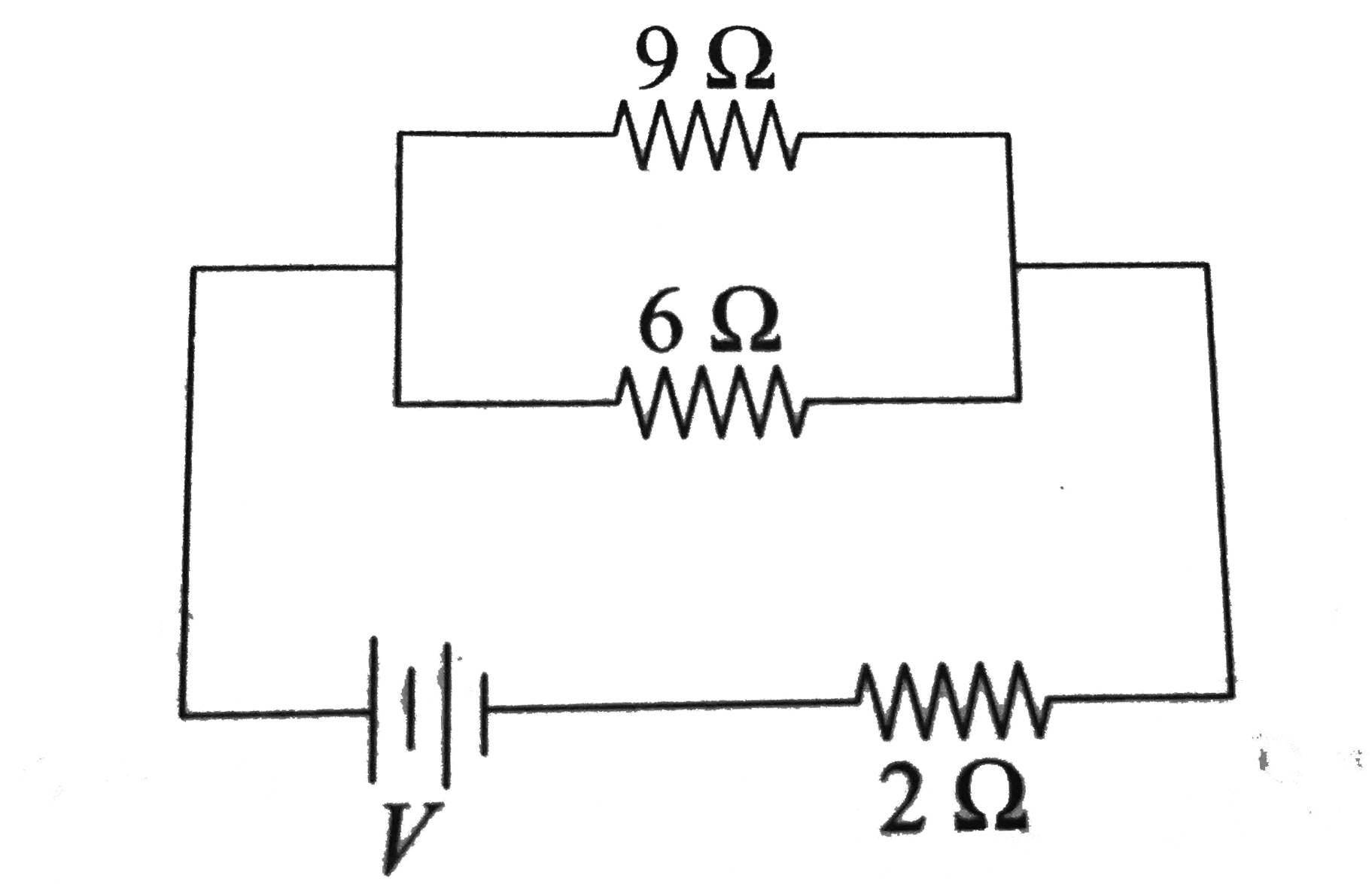
View Solution
