A resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the resistors and their values
We have two resistors in series:
- Resistor R1 = 6 Ω
- Resistor R2 = 4 Ω
Step 2: Calculate the equivalent resistance
Since the resistors are in series, the equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2
Req=6Ω+4Ω=10Ω
Step 3: Use Ohm's Law to find the current
Ohm's Law states that:
V=I×R
Where:
- V = total voltage across the circuit = 20 V
- I = current in the circuit
- R = equivalent resistance
Rearranging the formula to find the current (I):
I=VReq
Substituting the values:
I=20V10Ω=2A
Step 4: Calculate the potential difference across the 6 Ω resistor
The potential difference (V1) across the 6 Ω resistor can be calculated using Ohm's Law again:
V1=I×R1
Substituting the values:
V1=2A×6Ω=12V
Final Answer
The potential difference across the 6 Ω resistor is 12 V.
---
We have two resistors in series:
- Resistor R1 = 6 Ω
- Resistor R2 = 4 Ω
Since the resistors are in series, the equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2
Req=6Ω+4Ω=10Ω
Ohm's Law states that:
V=I×R
Where:
- V = total voltage across the circuit = 20 V
- I = current in the circuit
- R = equivalent resistance
I=VReq
Substituting the values:
I=20V10Ω=2A
The potential difference (V1) across the 6 Ω resistor can be calculated using Ohm's Law again:
V1=I×R1
Substituting the values:
V1=2A×6Ω=12V
The potential difference across the 6 Ω resistor is 12 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C)
22 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C) MULTIPLE CHOICE TYPE)
2 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (MULTIPLE CHOICE TYPE)
3 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
A resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the current in the circuit,
View SolutionThe potential drop across the 3Ω resistor is
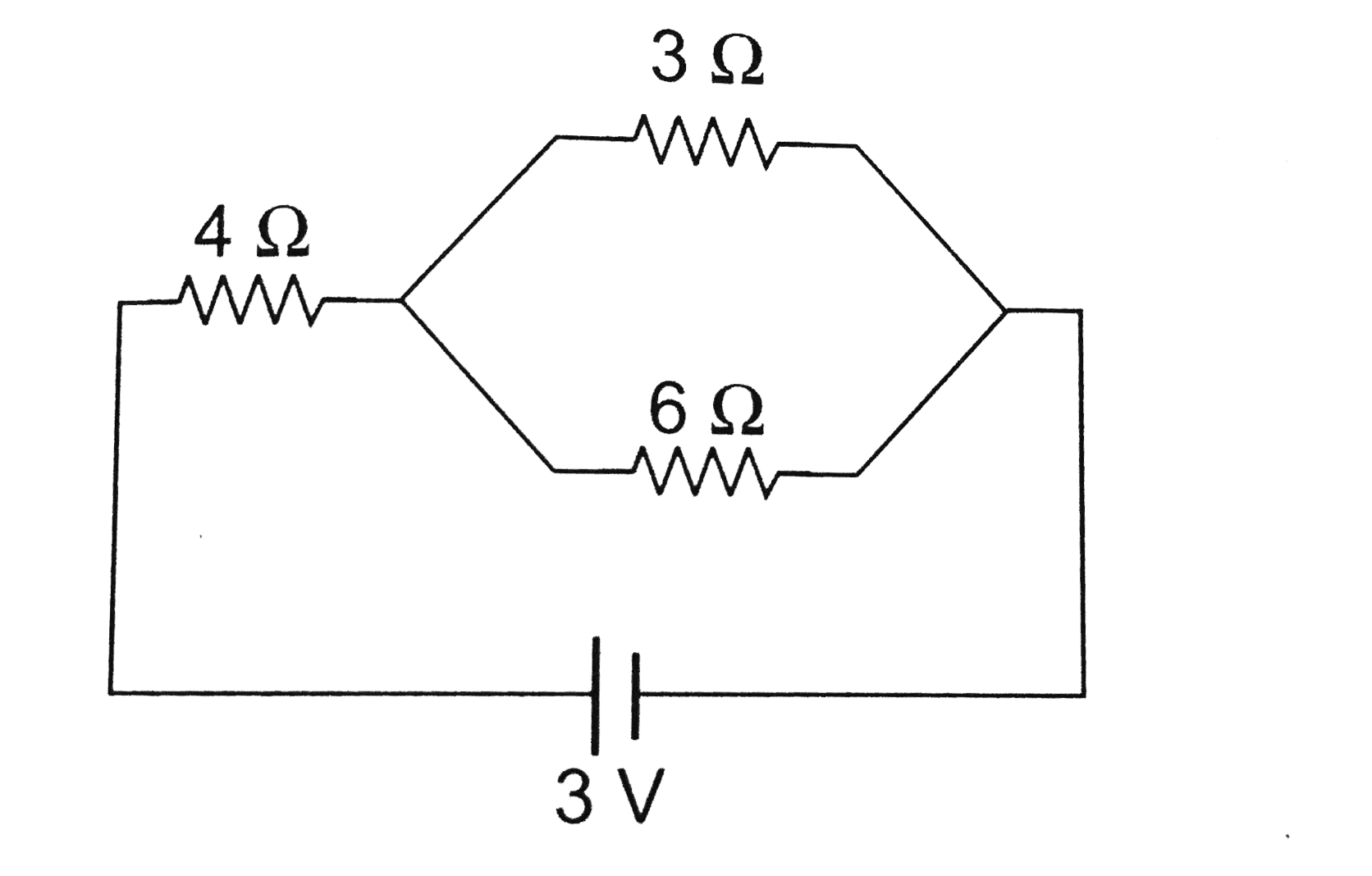
View SolutionDraw a circuit diagram of an electric circuit containing a cell, a key, an ammeter, a resistance of 2Ω in series with a combination of two resistors (4Ω each) in parallel and a voltmeter across the parallel combination. Will the potential difference across the 2Ω resistor be the same as that across the parallel combination of 4Ω resistors ? Give reason.
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
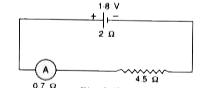
View SolutionA 4μF capacitor, a resistance of 2.5MΩ is in series with 12V battery. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [ Given In (2) = 0.693]
View SolutionIf the power dissipated in the 27Ω resistor in the circuit shown is 108 watt, the potential difference across the 4Ω resistor is
View SolutionThree resistors are connected to a 6 V battery as shown in the figure given below :
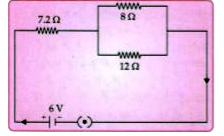
Calculate :
potential difference across the 7.2Ω resistor.
View SolutionThree resistors are connected to a 6 V battery as shown in the figure
Calculate:
potential difference across the 7.2 ohm resistor
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View SolutionA resistor circuit is constructed such that 12 resistor are arranged to form a cube as shown in fig. Each resistor has a resistance of 2Ω. The potential difference of 30V is applied across two of the opposing points as shown
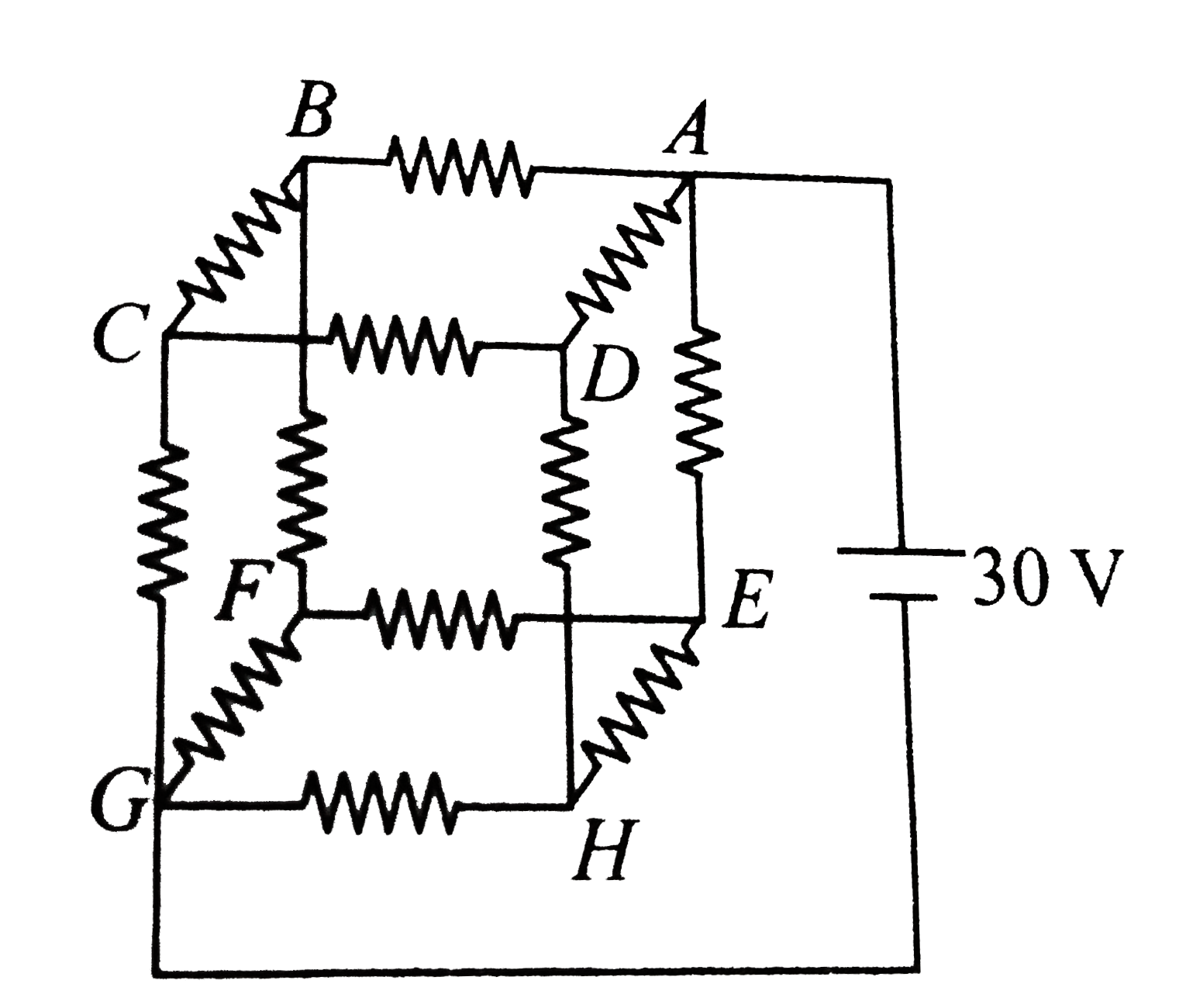
In question 20, the potential difference between the points C and G is
View Solution

