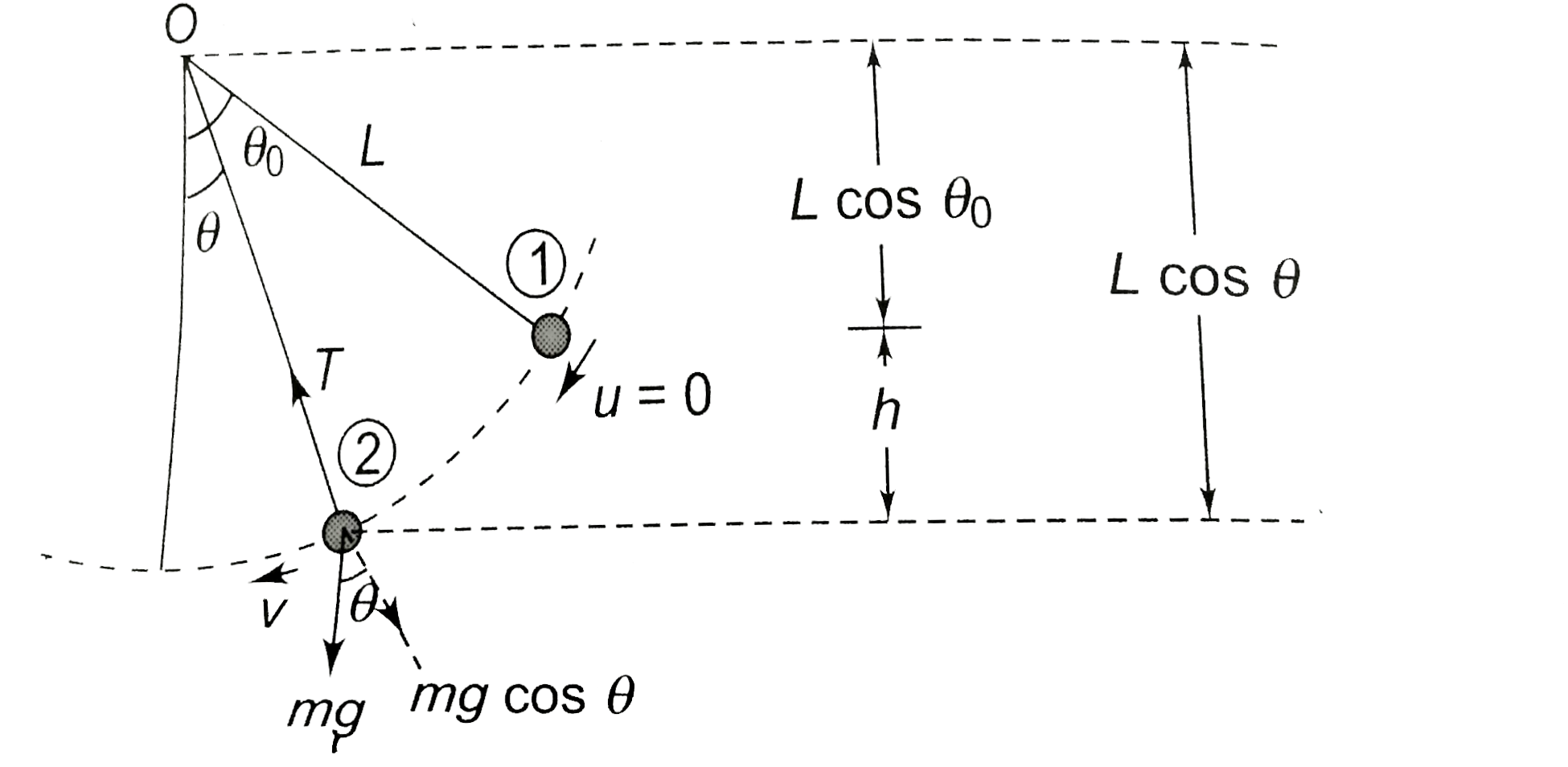
A 40 kg mass, hanging at the end of a rope of length l, oscillates in a vertical plane with an angular amplitude θ0. What is the tension in the rope when it makes en angle θ with the vertical ? If the breaking strength of the rope is 80 kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
At position (1),u=0
v2=u2+2gh=0+2gL(cosθ−cosθ0)
T−mgcosθ=mv2L=mL×2gL(cosθ−cosθ0)
T=mg[cosθ+2cosθ−2cosθ0]
=3mgcosθ−2mgcosθ0
=120gcosθ−80gcosθ0
when the mass is at the lowest point, tension in the string is maximum,
θ=0,T=Tmax=80g
T=120gcosθ−80gcosθ0
Tmax=120gcosθ−80gcosθ0
80g=120g−80gcosθ0=12⇒θ0=60∘
Topper's Solved these Questions
Similar Questions
A 40 kg mass, hanging at the end fo a rope of length l, oscillates in a vertical plane with an angular amplitude θ0. What is the tension in the rope when it makes en angle θ with the vertical ? If the breaking strength of the rope is 80kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
View SolutionA 40-kg mass hanging at the end of a rope of length l. Oscillates in a vertical plane with an angular of θ0. What is the tension in the rope when it makes an angle θ with the vertial ? If the breaking strength of the rope is 80 kg, what is the maximum angular amplitude with which the mass can oscillate without the rope breaking ?
View Solution
Knowledge Check
A fireman is sliding down with the help of a rope. If the breaking strength of the rope is 2mg3 where m is the mass of the man, the minimum acceleration with which the fireman can slide, so that the rope does not break, is :
Ag2Bg3Cg4D2g3An object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
A30.5 NB40.5 NC50.5 ND60.5 NA simple pendulum of length 'l' carries a bob of mass 'm'. If the breaking strength of the string is 3mg, the maximum angular amplitude from the vertical can be
A0∘B30∘C60∘D90∘
A boy of mass 40kg climbs up a rope with an acceleration of 1.2ms−2.What is the tension in the rope?
View SolutionA heavy block of mass M hangs in equilibrium at the end of a rope of mass m and length l connected to a celling. Determine the tension in the rope at a distance x from the ceiling.
View SolutionA mass of 10kg is suspended by a rope of length 2.8m from a ceiling. A force of 98N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
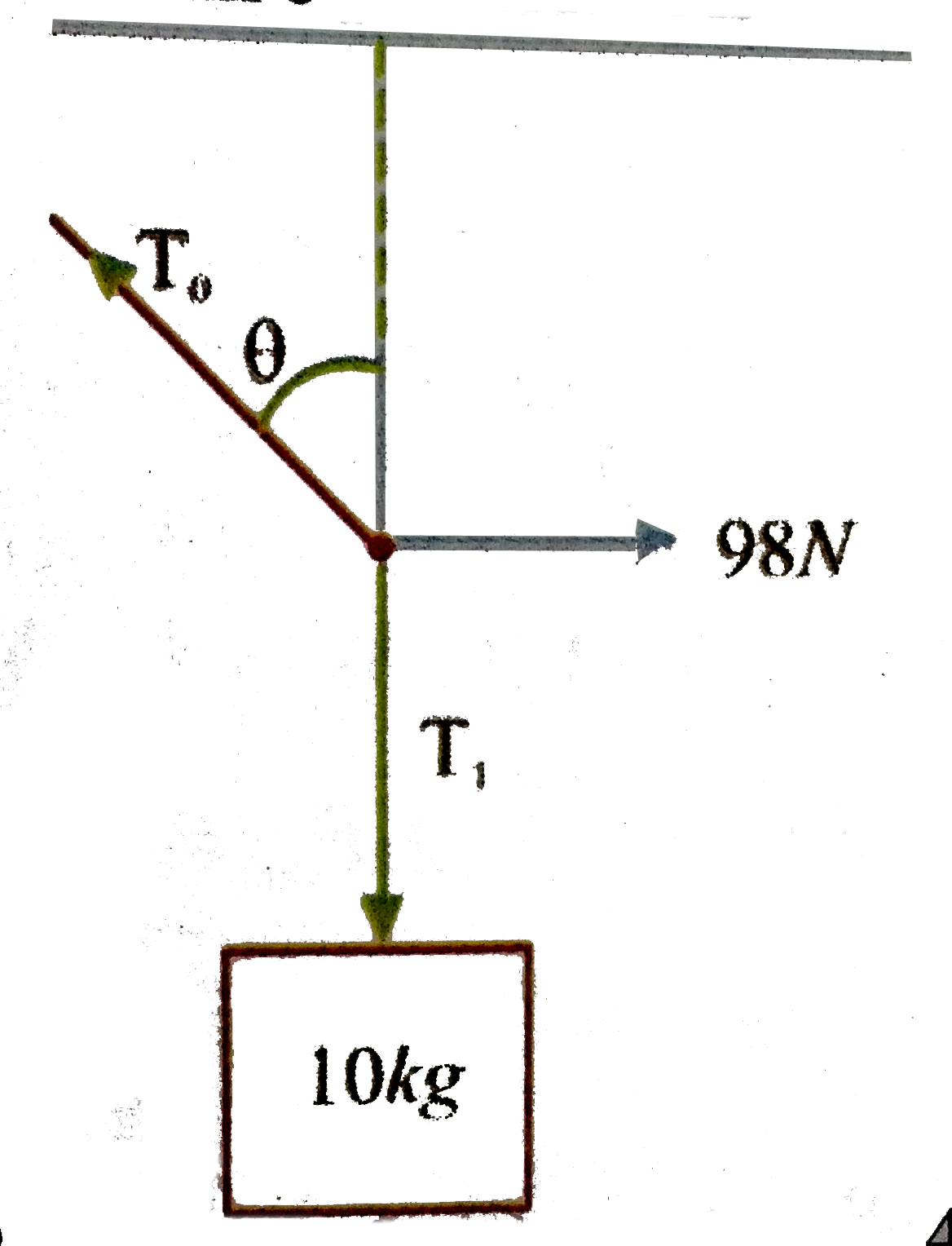 .
.
View SolutionA mass of 10 kg is suspended by a rope of length 2.8m from a ceiling. A force of 98 N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
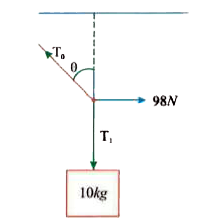
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
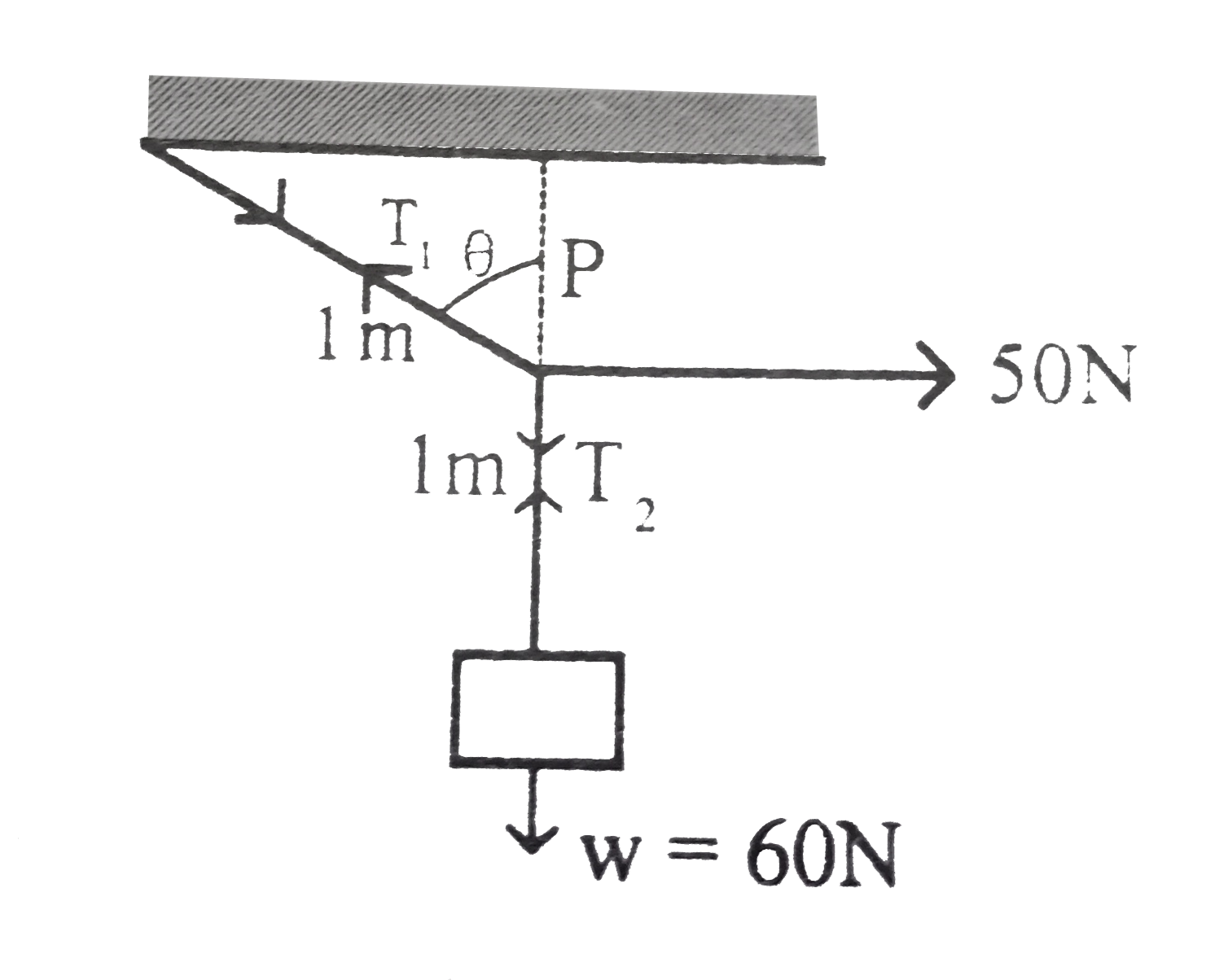
View Solution
