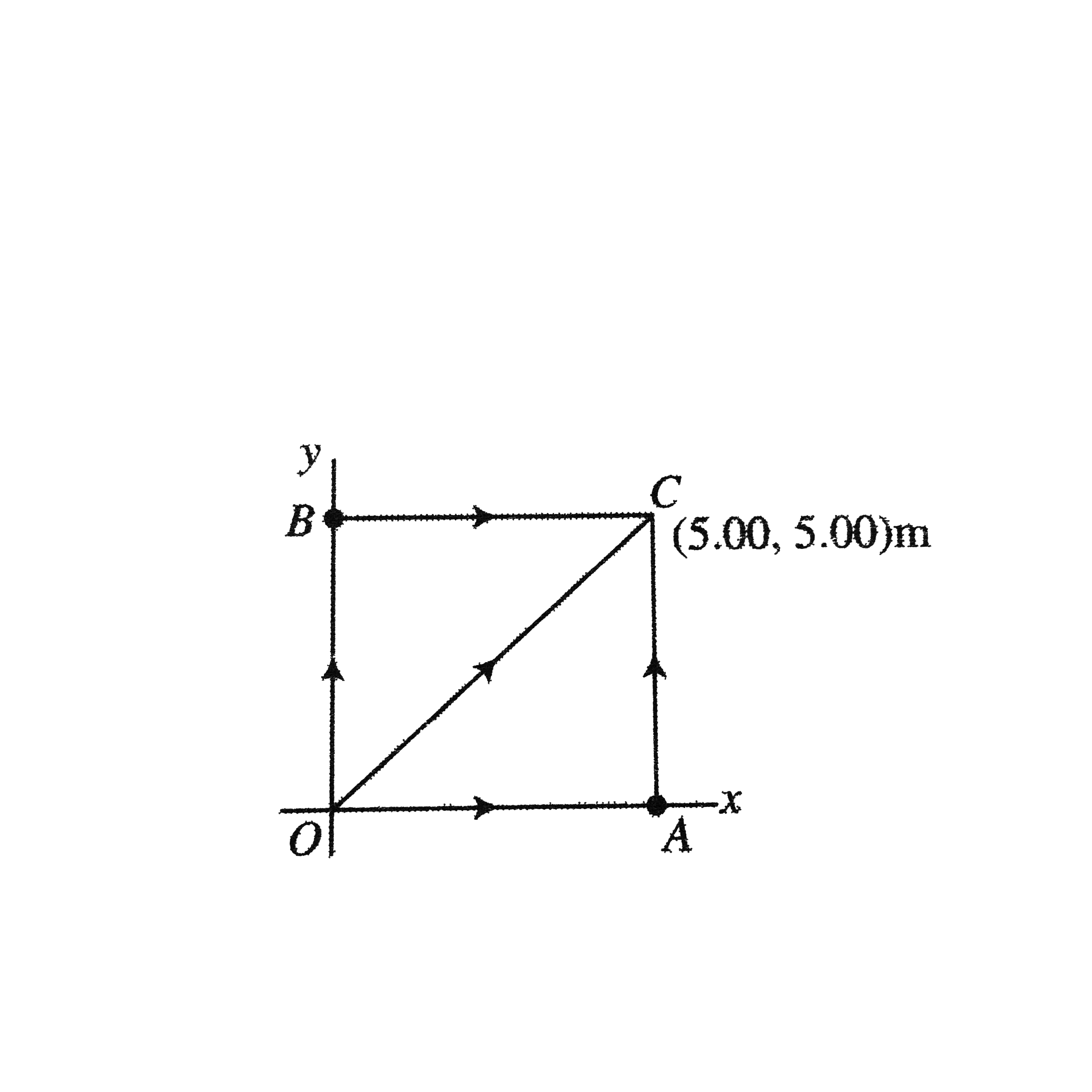
A 4.00−kg particle moves from the origin to position C, having coordinate x=5.00m and y=5m. One force on the particle is the gravitational force acting in the negative y direction. Using equation W=FΔrcosθ=→F.Δ→r, calculate the work done by the gravitional force on the particle as it goes from O to C along (a) OAC, (b) OBC, and (c) OC. Your results should all be identical. Why?
Fg=mg=(4.00kg)(10.0ms−2)=40.0N
a. Work done along OAC=Work along OA+Work along AC
=Fg(OA)cos90.0∘+Fg(AC)cos180∘
=(40.0N)(5.00m)cos90∘+(40.0N)(5.00m)cos180∘=−200J
b. Work done along OBC=W along OB+W along BC
=(40.0)(5.00m)cos180∘+(40.0N)(5.00m)cos90.0∘=−200J
c. Work done along OC=FgOCcos135∘
=(40.0N)(5.00×√2m)(−1√2)=−200J
Work done is same in all cases because gravitational force is a conservative force.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
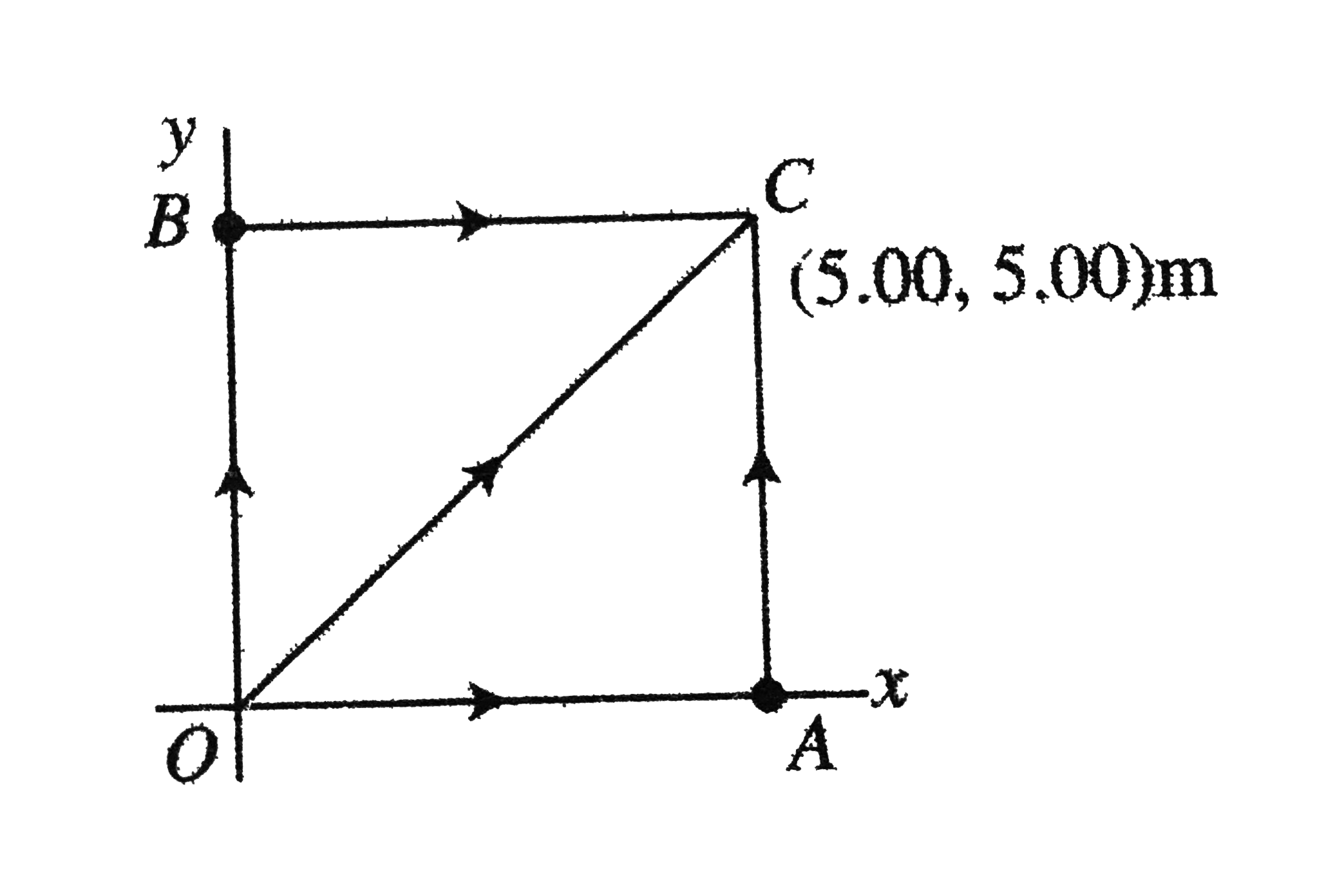
A force acting on a particle moving in the x-y plane is given by →F=(2yˆi+x2ˆj)N, where x and y are in meters. The particle moves from the origin to a final position having coordinates x=5.00m as shown in figure. Calculate the work done by →F on the particle as it moves along (a) OAC, (b) OBC, and (c) OC. (d) Is →F conservative or non-conservative? Explain.
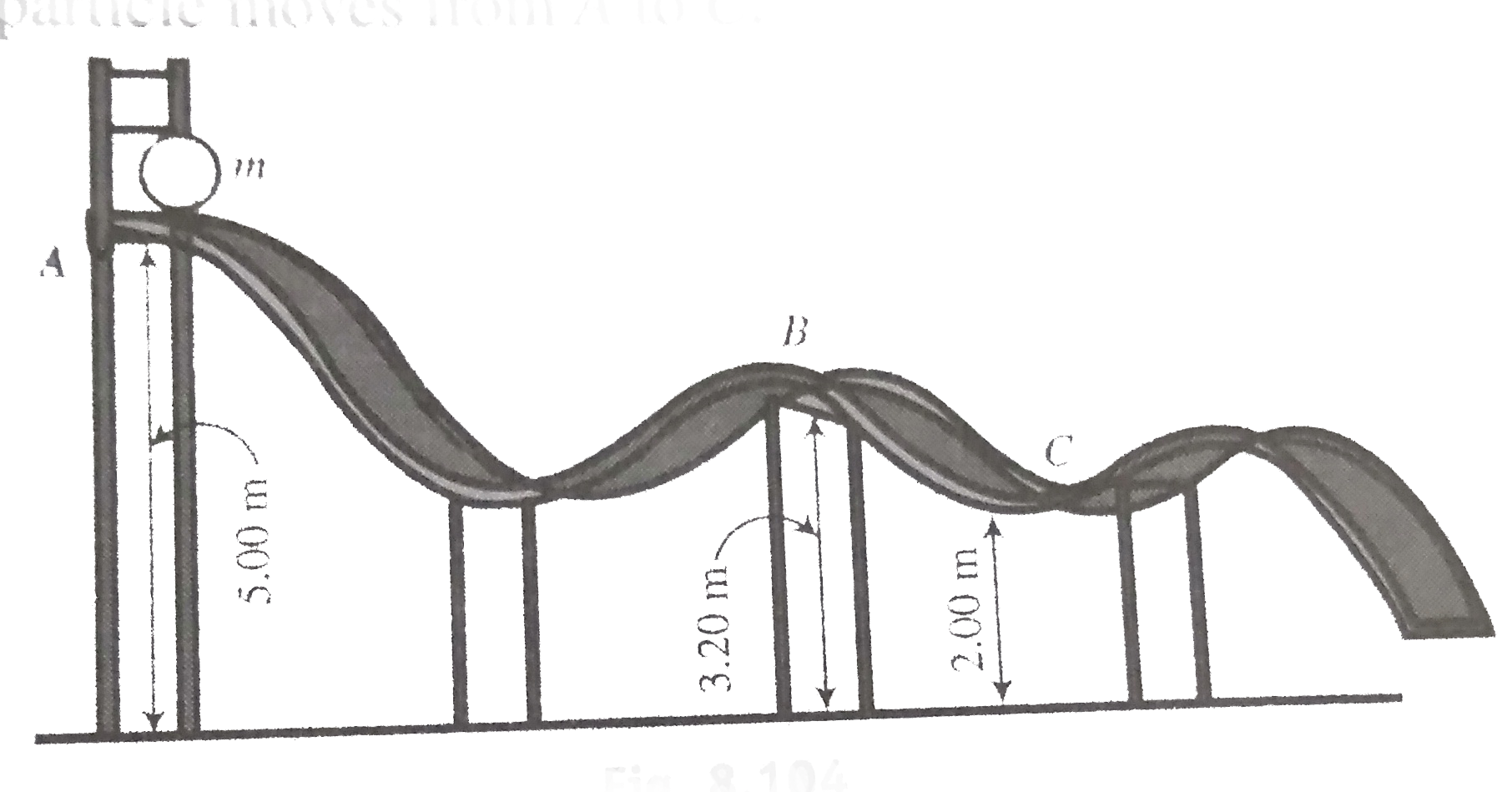
View SolutionA particle of mass m=5.00kg is released from point A and it slides on the frictionless track shown in figure. Determine (a) the particle's speed at points B and C and (b) the net work done by the gravitational force as the particle moves from A to C.
View Solution
Knowledge Check
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
A particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionA particle moves in x-y plane in figure under the influence of a friction force with magnitude 3.00N and acting in the direction opposite to the particle's displacement. Calculate the work done by the friction force on particle as it moves along the following paths: (a) path OA followed by AC (b) path OA followed by AC and the return path CO, (c) path OC followed by the return path CO, and (d) each of your three answers should be non-zero. What is the significant of this observation?

View SolutionA uniform force of (3ˆi+ˆj) N acts on a particle of mass 2kg. Hence, the particle is displaced from position (2ˆi+ˆk)m to position (4ˆi+3ˆj−ˆk)m. The work done by the force on the particle is
View SolutionThe gravitational field in a region is given by E=(2ˆi+3ˆj)N/kg.
Find the work done by the gravitational filed when a particle of mass 1kg is moved on the line 3y+2X=5 from (1m,1m) to (−2m,3m).
View SolutionThe gravitational field in a region is given by →E=(10Nkg−1)(→i+→j). Find the work done by an external agent to slowly shift a particle of mass 2 kg from the point (0,0) to a point (5m,4m)
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionThe work done by the forces →F=2ˆi−3ˆj+2ˆk in moving a particle from (3,4,5) to (1,2,3) is (A) 0 (B) 32 (C) −4 (D) −2
View Solution
