A 4kg block is attached to a vertical rod by means of two strings of equal length. When the system rotates about the axis of the rod, the strings are extended as shown in figure.
(a) How many revolutions per minute must the system make in order for the tension in the upper string to be 200N ?
(b) What is the tension in the lower string then ?

The correct Answer is:A, B, C

T1cosθ+T2cosθ=mrω2
ω=(2nπ)
Here, n=number of revolutions per second. Substituting the proper values in Eq. (i) ,
200(35)+T2×(35)=(4)(3)(2nπ)2
or 600+3T2=240n2π2
Further, T1sinθ=T2sinθ+mg
or 200×45=T2×45+4×10
or 800=4T2+200
Solving Eqs. (ii) and (iii) we get,
T2=150N and n=0.66rps
=39.6rpm
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.3
4 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Assertion And Reason
28 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.1
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Find the tension in the strings AC and BC shown in figure.

View SolutionFor the system shown in figure, the tensions in the string
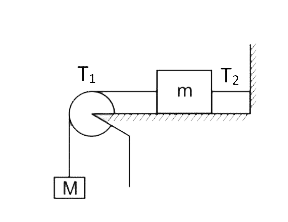
View SolutionThe tension T in the string shown in figure is

View SolutionIn the following figure, if the tension in the string AB is 51N, then the tension in the string BC will be :-
View SolutionThe tension in the string connected between blocks is

View Solution
A rod is supported horizontally by means of two strings of equal length as shown in figure. If one of the string is cut. Then tension in other string at the same instant will.
View SolutionA block of weight W is supported by three strings as shown in figure. Which of the following relations is true for tension in the string ? (Here, T1,T2 and T3 are the tension in the strings A,B and C respectively)

View SolutionA kite is attached to a string. Find the length of the string , when the height of the kite is 60 m and the string makes an angle 30∘ with the ground .
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View Solution1.Consider the situation shown in figure (6-E2).Calculate (a) the acceleration of the 1⋅0kg blocks,(b) the tension in the string connecting the 1.0kg blocks and (c) the tension in the string attached to 0.50kg.
View Solution
