A 5 kg collar is attached to a spring of spring constant 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
(a) The periodm of oscillation as given by Eq. (14.21) is,
T=2π√mk=2π√5.0kg500 N m−1
=(2π/10)s
=0.63s
(b) the velocity of the collar executing executting SHM is given by
v(t)=−Aωsin(ωt+ϕ)
The maximum speed is given by,
vm=Aω
=0.1×√km
=0.1×√500 N m−15kg
=1ms−1
and it occurs at x=0
(c) The acceleration of the collar at the displacement x(t) from the equilibrium is given by,
a(t)=−ω2x(t)
=−kmx(t)
Therefore, the maximum acceleration is,
amax=ω2A
=500 N m−15 kg×0.1m
=10ms−2
and it occurs at the extremitles.
Topper's Solved these Questions
Similar Questions
A 2.5 kg collar is attached to a spring of spring constant 250Nm−1 . It slides without friction over a horizontal surface . It is displaced from its equilibrium position by 220 cm and releasd. Calculate the period of osciallation and the maximum speed.
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View Solution
Knowledge Check
- Question 1 - Select One
A 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
Aπ5sBπ2sCπsD2πs - Question 2 - Select One
A 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
A10ms−2B100ms−2C200ms−2D0.1ms−2
A 10 kg collar is attached to a spring of spring constant 1000Nm−1 . It slides without friction over a horizontal surface. If is displaced from its equilibrium position by 20 cm and released . Calculate
(a) The period of oscillation (b) The maximum speed
Hint :T=2π√mk,vm=Aω=A√kmView SolutionA 5 kg colloar is attached to a sprinig of spring constatn 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by oscillations (b) The maximum speed and © maximum acceleration of the collar.
View SolutionA 5kg collar is attached to a spring . It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 10 cm and released , its maximum speed is 1ms−1 Calculate
(a) Spring constant
(b) The period of oscillation
(c ) Maximum acceleration of the collar
Hint :m=5kg,A=0.1m,k=?,T=?or a=?,vm=1ms−1
vm=Aω=A√km
Find k,
T=2π√mk
amax=ω2A=kmAView SolutionA 4 kg roller is attached to a massless spring of spring constant k = 100 N/m. It rolls without slipping along a frcitionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. It rolls without slipping along a frictionless horizontal road. The roller is displaced from its equilibrium position by 10 cm and then released. Its maximum speed will be
View SolutionA tolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?
 View Solution
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
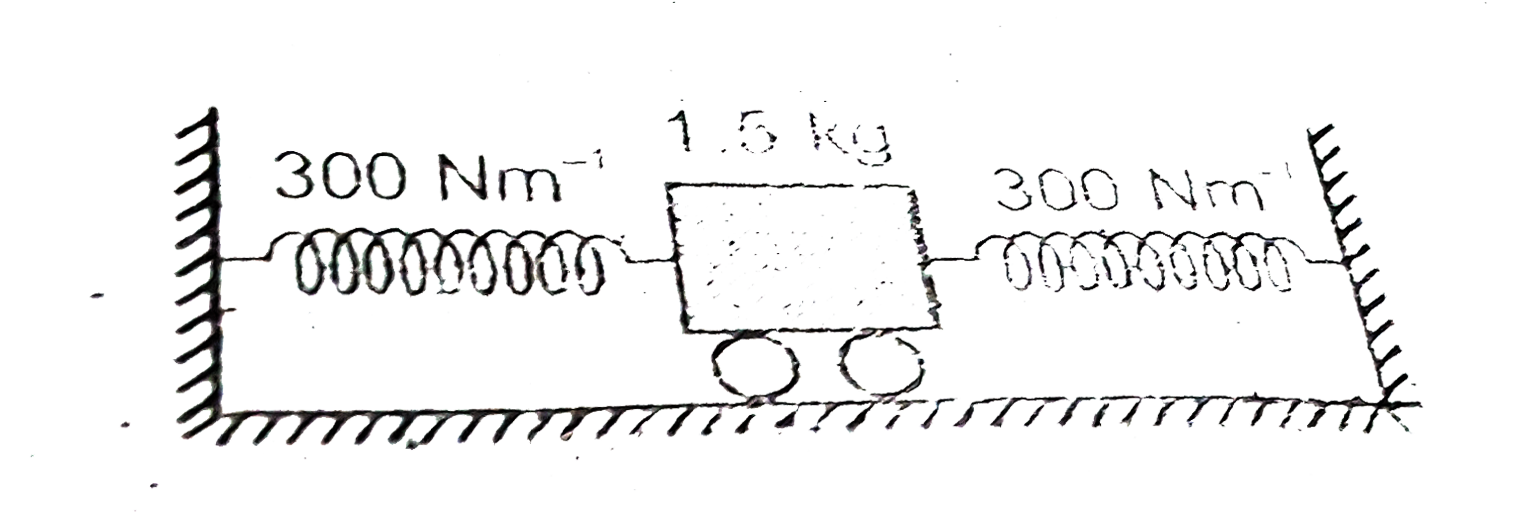 View Solution
View Solution

