Plot the corresponding reference circle for each of the following simple hoarmonic motions. Indicate the intial position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case is in cm and t is in s ).
(a) (b) (c) (d)
(a) x = 2 cos
Radius of the reference circle, r = amplitude of SHM = 2 cm,
At t = 0, x = - 2 sin
Also
The reference circle is, thus, as plotted below.
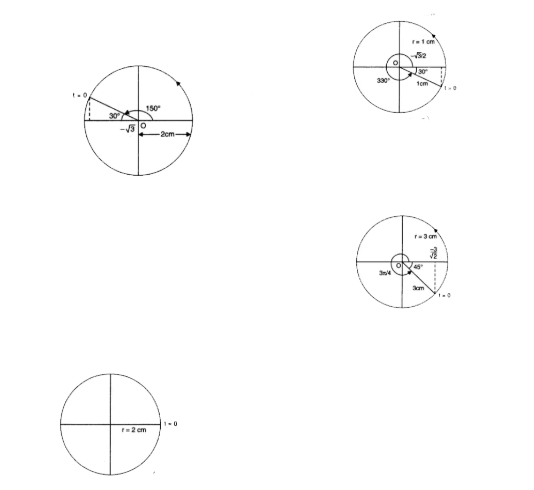
(b)
Radius of circle, r = amplitude of SHM = 1 cm.
At t = 0, x = cos
Also
The reference circle is, thus as plotted below
(c )
Here, radius of reference circle, r = 3 cm and at t = 0, x = 3
Therefore, the reference circle is being shown below.
(d) x = 2 cos
Radius of reference circle, r = 2 cm and at t = 0, x = 2 cm
The reference circle is plotted below.
Topper's Solved these Questions
Similar Questions
Plot the corresponding reference circle for given SHM, indicate the initial (t=0) position of the paritcle, the radius of the circle , and the angular speed of the rotating paritcle. Consider anticlockwise direction for rotation. x=−3sin(2t+π4) (Express in the form , x= Acos ( omega t + phi)).
View SolutionPlot the corresponding reference circle for given SHM x=2cos(π3−t) .Indicate the initial (t−0) position of the particle , the radius of the circle and the angular speed of the rotating particle . Consider anticlockwise direction for rotation.
Hint : x=2cos(π3−t)=2cos(t−π3) as cos(−θ)=cosθ . Compare with x=Acos(ωt+ϕ)View Solution
Knowledge Check
- Question 1 - Select One
A partilce is executive simple harmonic motion given by
x=5sin(4t−π6)
The velocity of the particle when its displacement is 3 units isA2π3 unitsB5π6 unitsC20 unitsD16 units - Question 2 - Select One
The displacement of a particle executing simple harmonic motion is given by
x=3sin(2πt+π4)
where x is in metres and t is in seconds. The amplitude and maximum speed of the particle isA3m, 2πms−1B3m, 4πms−1C3m, 6πms−1D3m, 8πms−1 - Question 3 - Select One
The displacement of a particle in S.H.M. is given by x=Bsin(ωt+α). The initial position (at time t=0), of the particle is the initial phase angle if the angular frequency of the particle is πrad/s ?
Aπ2Bπ4Cπ6Dπ5
A particle is subjected to two simple harmonic motions.
x1=4.0sin(100πt) and x2=3.0sin(100πt+π3)
Find
(a) the displacement at t=0
(b) the maximum speed of the particle and
(c ) the maximum acceleration of the particle.View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated in the · figure. The simple harmonic motion of the X-projection of the radius vector of the rotating particle Pis
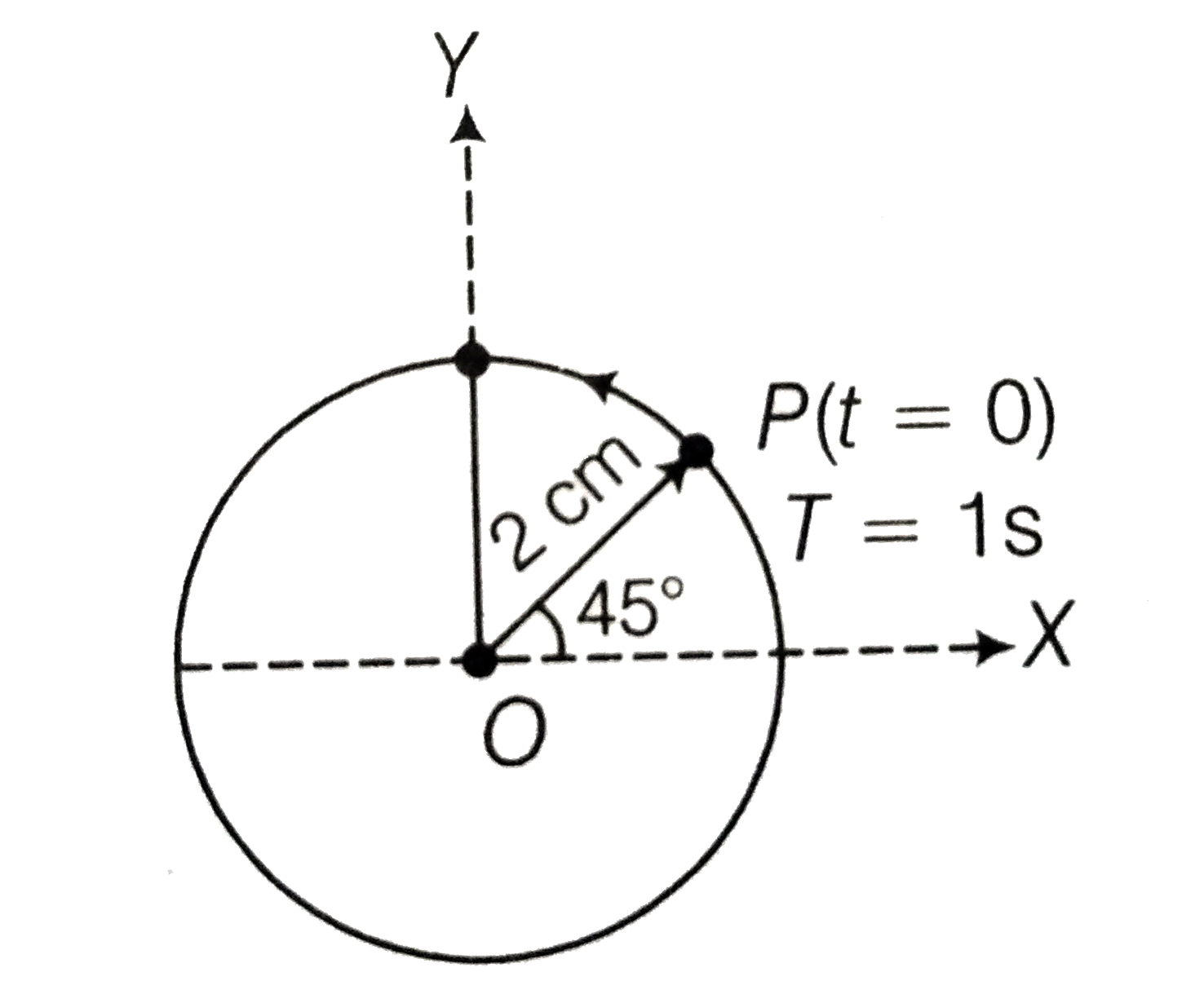 View Solution
View SolutionThe equation of particle executing simple harmonic motion is x=(5m)sin[(πs−1)t+π3]. Write down the amplitude, time period and maximum speed. Also find the velocity at t=1s.
View SolutionPosition-time relationship of a particle executing simple harmonic motion is given by equation
x=2sin(50πt+2π3) where x is in meters and time t is in seconds.
What is the position of particle at t=0.5s ?View SolutionPosition-time relationship of a particle executing simple harmonic motion is given by equation
x=2sin(50πt+2π3) where x is in meters and time t is in seconds.
What is the position of particle at t=1s ?View Solution

