A 6.5 m long ladder rests against as vertical wall reaching a height of 6.0 m. A 60 kg man stands hlf way up the ladder. A. Find the torque of the force exerted by the man on the ladder bout the upper end of the ladder. b.Assuming the weight of the ladder of be negligible as compared to the man and assuming the wall to be smooth find the force exerted by the ground on the ladder.
The correct Answer is:A, B, C, D
To solve the problem step-by-step, we will break it down into two parts as specified in the question.
Part A: Finding the Torque of the Force Exerted by the Man on the Ladder about the Upper End of the Ladder
1. Identify the Forces Acting on the Ladder:
- The weight of the man (W) is acting downwards at the midpoint of the ladder. The weight can be calculated as:
W=mg=60kg×9.8m/s2=588N
2. Determine the Geometry of the Ladder:
- The length of the ladder (L) is 6.5 m, and it reaches a height (h) of 6.0 m against the wall.
- The horizontal distance (d) from the base of the ladder to the wall can be found using the Pythagorean theorem:
d=√L2−h2=√(6.5)2−(6.0)2=√42.25−36=√6.25=2.5m
3. Calculate the Angle of the Ladder:
- The angle (θ) can be calculated using:
sin(θ)=hL=6.06.5
- Thus, θ=arcsin(6.06.5).
4. Calculate the Torque (τ) about the Upper End of the Ladder:
- The torque due to the weight of the man about the upper end of the ladder is given by:
τ=W⋅(L2)⋅sin(θ)
- Substituting the values:
τ=588N⋅(6.52)⋅sin(θ)
- Calculate sin(θ):
sin(θ)=hL=6.06.5≈0.923
- Therefore, substituting this back:
τ=588⋅3.25⋅0.923≈1685.1N m
Part B: Finding the Force Exerted by the Ground on the Ladder
1. Identify the Forces Acting on the Ladder:
- The vertical force exerted by the ground (R) must balance the weight of the man. Therefore:
R=W=588N
2. Determine the Horizontal Force:
- Since the wall is smooth, there is no friction at the wall. The horizontal force exerted by the ground (F) must balance the horizontal component of the force exerted by the man.
3. Calculate the Torque about the Base of the Ladder:
- The torque due to the weight of the man about the base of the ladder is:
τman=W⋅(L2)⋅sin(θ)
- The torque due to the horizontal force (F) about the base of the ladder is:
τF=F⋅L⋅cos(θ)
4. Set the Torques Equal:
- For the ladder to be in equilibrium:
τman=τF
- Therefore:
588⋅3.25⋅sin(θ)=F⋅6.5⋅cos(θ)
5. Solve for F:
- Rearranging gives:
F=588⋅3.25⋅sin(θ)6.5⋅cos(θ)
- Substitute sin(θ) and cos(θ):
F=588⋅3.25⋅6.06.56.5⋅2.56.5=588⋅3.25⋅6.02.5⋅6.5
- Calculate F to find the horizontal force exerted by the ground.
- The weight of the man (W) is acting downwards at the midpoint of the ladder. The weight can be calculated as:
W=mg=60kg×9.8m/s2=588N
- The length of the ladder (L) is 6.5 m, and it reaches a height (h) of 6.0 m against the wall.
- The horizontal distance (d) from the base of the ladder to the wall can be found using the Pythagorean theorem:
d=√L2−h2=√(6.5)2−(6.0)2=√42.25−36=√6.25=2.5m
- The angle (θ) can be calculated using:
sin(θ)=hL=6.06.5
- Thus, θ=arcsin(6.06.5).
- The torque due to the weight of the man about the upper end of the ladder is given by:
τ=W⋅(L2)⋅sin(θ)
- Substituting the values:
τ=588N⋅(6.52)⋅sin(θ)
- Calculate sin(θ):
sin(θ)=hL=6.06.5≈0.923
- Therefore, substituting this back:
τ=588⋅3.25⋅0.923≈1685.1N m
- The vertical force exerted by the ground (R) must balance the weight of the man. Therefore:
R=W=588N
- Since the wall is smooth, there is no friction at the wall. The horizontal force exerted by the ground (F) must balance the horizontal component of the force exerted by the man.
- The torque due to the weight of the man about the base of the ladder is:
τman=W⋅(L2)⋅sin(θ)
- The torque due to the horizontal force (F) about the base of the ladder is:
τF=F⋅L⋅cos(θ)
- For the ladder to be in equilibrium:
τman=τF
- Therefore:
588⋅3.25⋅sin(θ)=F⋅6.5⋅cos(θ)
- Rearranging gives:
F=588⋅3.25⋅sin(θ)6.5⋅cos(θ)
- Substitute sin(θ) and cos(θ):
F=588⋅3.25⋅6.06.56.5⋅2.56.5=588⋅3.25⋅6.02.5⋅6.5
- Calculate F to find the horizontal force exerted by the ground.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A 5-m long ladder when set against the wall of a house reaches a height of 4.8 cm.How far is the foot of the ladder from the wall?
View SolutionA ladder of length 50 m rests against a vertical wall, at a height of 30 m from the ground. Find the inclination of the ladder with the horizontal. Also find the distance between the foot of the ladder and the wall.
View Solution
Knowledge Check
A ladder is resting with a vertical wall at an angle of 30∘. If a man is ascending the ladder of at the rate of 6 feet/sec, then the rate at which the man is approaching the wall, is
A9 feet/secB2 feet/secC3 feet/secD6 feet/secA weightless ladder 6m long rests against a frictionless wall at an angle of 60∘ from the horizontal. A 60kg man standing on it is 2m from the top of the ladder. A horizontal force is applied at the lower end to keep it from slipping. The magnitude of the force is
A10√3NB20√3NC√320ND20√3N
A ladder 10m long rests against a vertical wall. If the foot of the ladder is 6m away from the wall and the ladder just reaches the top of the wall, how high is the wall?
View SolutionA 5.5m long ladder is leaned against a wall. The ladder reaches the wall to a height of 4.4m. Find the distance between the wall and the foot of the ladder.
View SolutionFoot of a 10 m long ladder leaning against a verticle wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
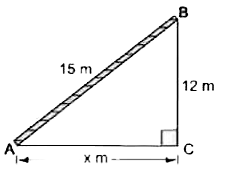
View SolutionA 15-m long ladder is placed against a wall to reach a window 12 m high.Find the distance of the ladder from the wall.
View SolutionA ladder leaning against a wall makes an angle of 60o with the ground. If the length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.
View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View Solution
