(a) A car starts moving (at point A) on a horizontal circular track and moves in anticlockwise sense. The speed of the car is made to increase uniformly. The car slips just after point D. The figure shows the friction force (f) acting on the car at points A, B, C and D. The length of the arrow indicates the magnitude of the friction and it is given that ∠D>∠B>∠C. At which point (A, B, C or D) the friction forces represented is certainly wrong ?
![(a) A car starts moving (at point A) on a horizontal circular track and moves in anticlockwise sense. The speed of the car is made to increase uniformly. The car slips just after point D. The figure shows the friction force (f) acting on the car at points A, B, C and D. The length of the arrow indicates the magnitude of the friction and it is given that angleD gt angleB gt angleC. At which point (A, B, C or D) the friction forces represented is certainly wrong ? (b) A particle is moving along an expanding spiral (shown in fig) such that the normal force on the particle [i.e., component of force perpendicular to the path of the particle] remains constant in magnitude. The possible direction of acceleration(veca)of the particle has been shown at three points A, B and C on its path. At which of these points the direction of acceleration has been represented correctly. (c) A particle is moving in XY plane with a velocity . vecv = 4hati + 2thatj ms^(-1) . Calculate its rate of change of speed and normal acceleration at t = 2 s.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C03_E01_036_Q01.png)
(b) A particle is moving along an expanding spiral (shown in fig) such that the normal force on the particle [i.e., component of force perpendicular to the path of the particle] remains constant in magnitude. The possible direction of acceleration(→a)of the particle has been shown at three points A, B and C on its path. At which of these points the direction of acceleration has been represented correctly.

(c) A particle is moving in XY plane with a velocity . →v=4ˆi+2tˆjms−1 . Calculate its rate of change of speed and normal acceleration at t = 2 s.
The correct Answer is:(a) At C
(b) At C
(c) √2m/s2and√2m/s2
Topper's Solved these Questions
Similar Questions
A car starts moving from rest on a horizontal circular road of radius of curvature R at . The speed of the car is increasing at a constant rate a. The coefficient of friction between the road and the tyres of the car is The car starts slipping at timet=t0 . Then t0 is equal to:
View SolutionA car goes on a horizontal circular road of radius R. The speed of car is increasing at constant rate a m/s2. If the friction coefficient between the road and the tyre is μ, then the limiting speed of car is
View Solution
Knowledge Check
A car starts moving from rest on a horizontal circular road of radius of curvature R at . The speed of the car is increasing at a constant rate a. The coefficient of friction between the road and the tyres of the car is The car starts slipping at timet=t0 . Then t0 is equal to:
A.4√μ2g2R2aB.4√R2(μ2g2−a2)aC.4√R2(a2−μ2g2)aD.4√R2(μ2g2+a2)aA car is moving along a road with a uniform speed of 20 km/hour. The net force acting on the car is
Athe driving force (P) which drives the car in the forward directionBthe opposing (frictional) force (f),opposite to the direction of motion of the carCzeroDP+FA car is moving with velocity v on circular turn of radius R. Mass of the car is m. Evaluate the negative lift (FL) acting on the car
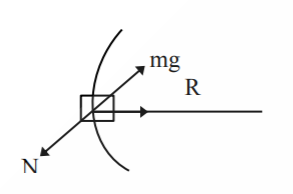 Amv2μR−2mgBmv22μR−2mgCmv2μR−mgDmv23μR−mg
Amv2μR−2mgBmv22μR−2mgCmv2μR−mgDmv23μR−mg
A car goes on a horizontal circular road of radius R. The speed of car is increasing at constant rate a m/s2. If the friction coefficient between the road and the tyre is μ, then the limiting speed of car is
View SolutionA car is moving along a circle with constant speed on an inclined plane as shown in diagram. Then friction force on car will be in horizontal direction at least at one point :

View SolutionA car moving towards North. What will be the direction of force of friction acting on this car due to surface of road ?
View SolutionA car is moving along a circle with constant speed on an inclined plane as shown in diagram. Then friction force on car will be in horizontal direction at least at one point :

View SolutionA car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is h, and the separation between its inner and outer wheels is d The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .
.
View Solution
