(a) A circular current carrying coil has a radius R. Find magnetic field (a) at centre and (b) along the axis of coil distant √3R from centre. The coil is having N turns and carriers a current i.
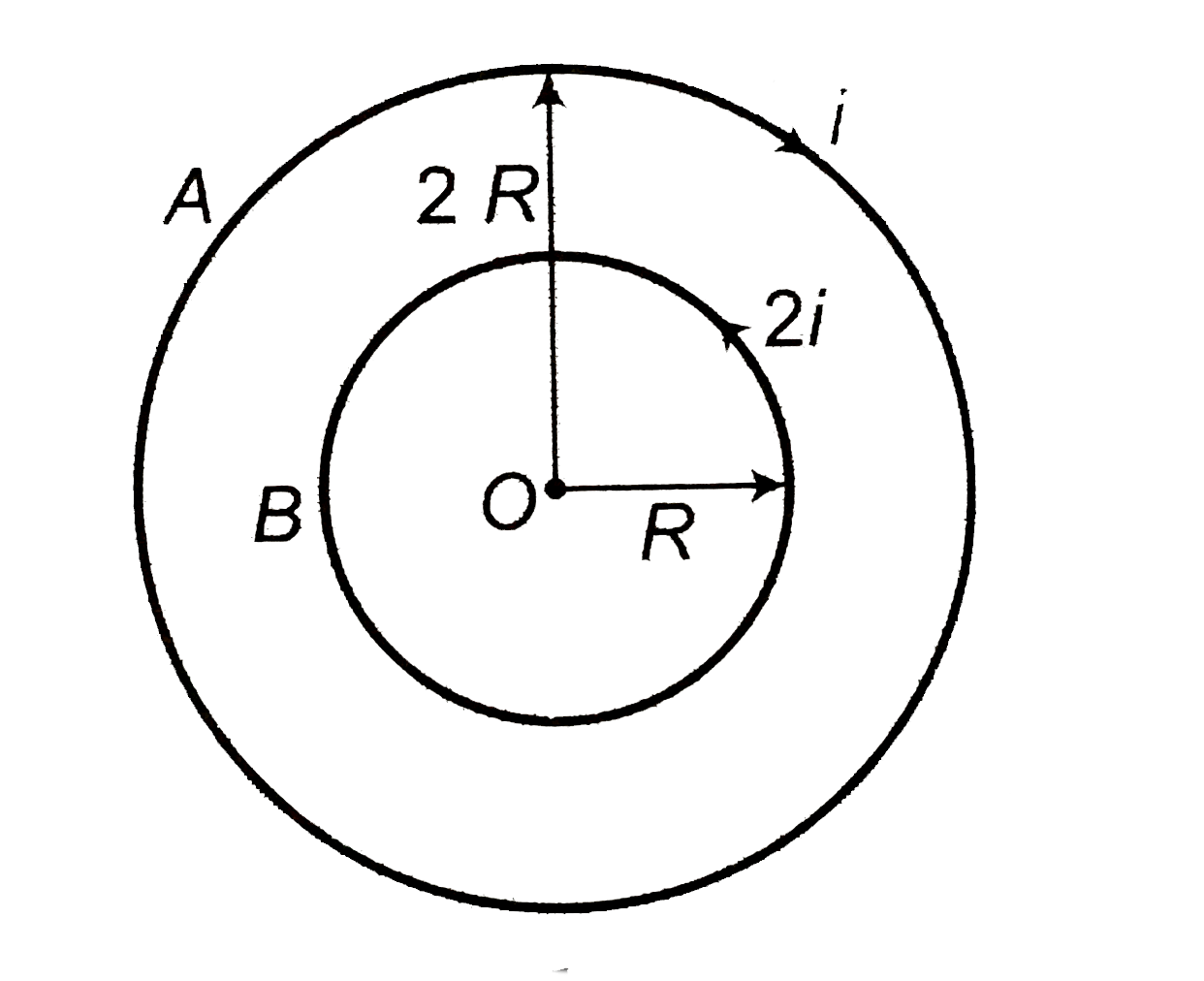
(b) Two concentric coil A and B, having current i and 2i and radii 2R and R are placed as shown. Find magnetic field at common centre.
(c) In previous problem, if planes of coil are perpendicular to each other, find magnetic field at common centre.
(d) A charge q distributed uniformely over a circular ring of radius R. The ring rotates about its axis with an angular velocity ω. find the magnetic field (a) at centre and (b) at distance √3R from centre, along the axis.
(a) (i) Magnetic field at centre of coil
BC=μ0Ni2R
(ii) Magnetic field at point P, on the axis of coil at distance x from centre
BP=μ0NiR22(R2+x2)3/2=μ0NiR22{R2+(√3R)2}3/2
=μ0NiR22(4R2)3/2=μ0NiR22×2√2R3=μ0Ni4√2R
(b) 
At O:
B1=μ0(2I)2R=μ0iR,⊙
B2=μ0i2(2R)=μ0i4R,⊗
BO=B1−B2=2μ0i4R,⊙
(c) If planes of coils are ⊥ar, B1 and B2 will be ⊥ar
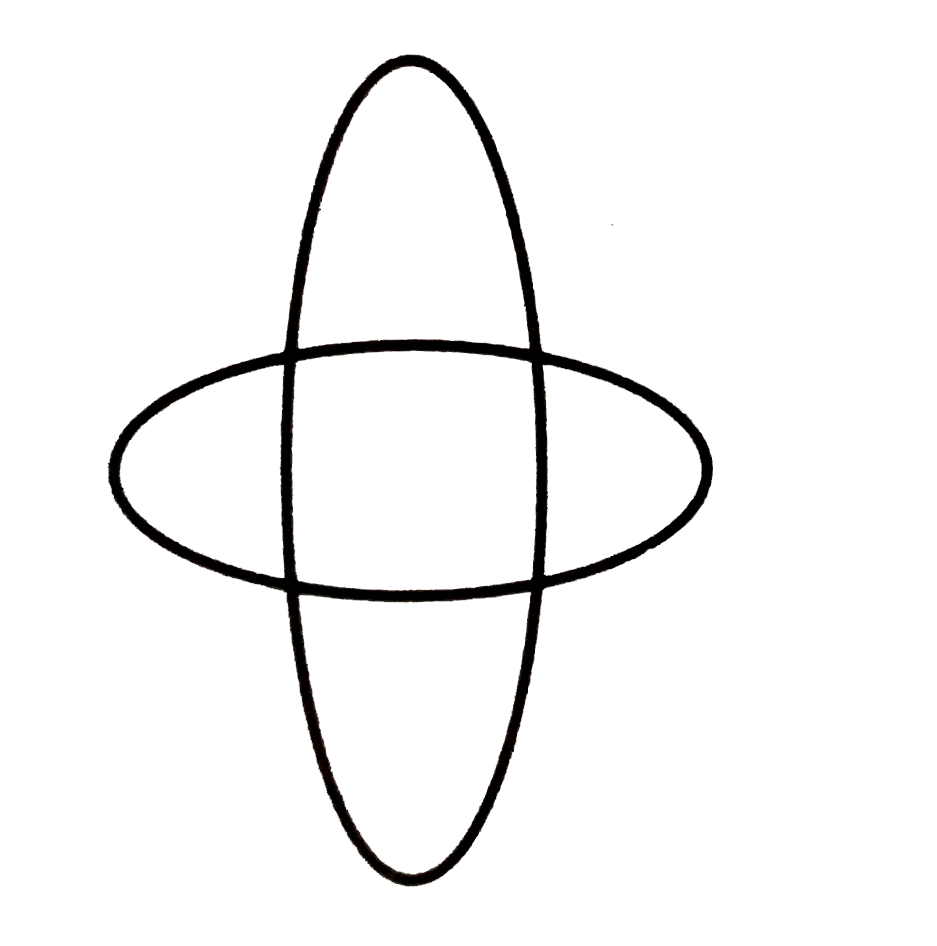
BO=μ0iR√(1)2+1(4)2
=√17μ0i4R
(d) Here current i=qT=q2π/ω=qω2π
(i) BC=μ0iR=μ0qω4πR
(ii) BP=μ0iR22[R2+(√3R)2]3/2
=μ0iR24√2R3=μ0i4√2R=μ0qω8√2πR
Topper's Solved these Questions
Similar Questions
A circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View Solution
Knowledge Check
- Question 1 - Select One
A circular current-carrying coil has a radius R. The distance from the centre of the coil, on the axis, where B will be 1/8 of its value at the centre of the coil is
AR√3B√3RC2√3RD2R√3 - Question 2 - Select One
Radius of current carrying coil is 'R'. Then ratio of magnetic fields at the centre of the coil to the axial point, which is R√3 distance away from the centre of the coil :-
A1:1B1:2C1:4D8:1 - Question 3 - Select One
A circular coil of radius 2R is carrying current I. The ratio of magnetic fields at the centre of coil and at a point at a distance 6R from centre of coil on axis of coil is
A10B10√10C20√5D20√10
A circular coil of wire of radius 'r' has 'n' turns and carries a current 'I'. The magnetic induction (B) at a point on the axis of the coil at a distance √3r from its centre is
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
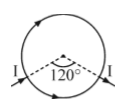 View Solution
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
 View Solution
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
View Solution

