A ball dropped from a point P crosses a point Q in t seconds. The time taken by it to travel from Q to R, if PQ = QR.
t
√2t
2t
(√2−1)t
The correct Answer is:D
To solve the problem, we will analyze the motion of the ball dropped from point P to point Q and then from point Q to point R, where PQ = QR.
1. Understanding the Motion:
- A ball is dropped from point P and crosses point Q in time t.
- The distance PQ is equal to the distance QR.
2. Using the Equation of Motion:
- The distance fallen by the ball from P to Q can be calculated using the equation of motion:
PQ=12gt2
- Here, g is the acceleration due to gravity.
3. Distance from Q to R:
- Since PQ=QR, we can denote the distance QR as x, which is equal to PQ:
QR=12gt2
4. Total Distance from P to R:
- The total distance PR can be expressed as:
PR=PQ+QR=12gt2+12gt2=gt2
5. Finding the Time from Q to R:
- Let the time taken to travel from Q to R be t1.
- Using the equation of motion again for the distance QR:
QR=12gt21
- Since QR=12gt2, we can set the two equations equal:
12gt21=12gt2
- Simplifying gives:
t21=t2⋅2
- Therefore:
t1=√2t
6. Finding the Time from Q to R:
- The total time taken from P to R is:
t+t1=t+√2t=t(1+√2)
- The time taken from Q to R is:
t1=√2t−t=t(√2−1)
Final Answer:
The time taken by the ball to travel from Q to R is:
t(√2−1)
- A ball is dropped from point P and crosses point Q in time t.
- The distance PQ is equal to the distance QR.
- The distance fallen by the ball from P to Q can be calculated using the equation of motion:
PQ=12gt2
- Here, g is the acceleration due to gravity.
- Since PQ=QR, we can denote the distance QR as x, which is equal to PQ:
QR=12gt2
- The total distance PR can be expressed as:
PR=PQ+QR=12gt2+12gt2=gt2
- Let the time taken to travel from Q to R be t1.
- Using the equation of motion again for the distance QR:
QR=12gt21
- Since QR=12gt2, we can set the two equations equal:
12gt21=12gt2
- Simplifying gives:
t21=t2⋅2
- Therefore:
t1=√2t
- The total time taken from P to R is:
t+t1=t+√2t=t(1+√2)
- The time taken from Q to R is:
t1=√2t−t=t(√2−1)
The time taken by the ball to travel from Q to R is:
t(√2−1)
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Knowledge Check
Ten million electrons pass from point P to point Q m one micro second. The current and its direction is
 A1.6×10−14A, from point P to point QB3.2×10−14A from point P to point QC1.6×10−6A From point Q to PD3.2×10−12A from point Q to point P
A1.6×10−14A, from point P to point QB3.2×10−14A from point P to point QC1.6×10−6A From point Q to PD3.2×10−12A from point Q to point P
A particle is thrown vertically upwards from the surface of the earth. Let TP be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let TQ be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of TP,TQ and H, is :-
View SolutionAn object is taken from a point P to another point Q in a gravitational field:
View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:

View SolutionA car starts from a point P at time t = 0 seconds and stops at point Q. The distance x, in metres, covered by it, in t seconds is given by x=t2(2−t3)Find the time taken by it to reach Q and also find distance between P and Q.
View SolutionDoes the ray PQ starts from points Q ?
View SolutionDr. Bansal needs to determine the distance PQ across a river in and east-west direction as shown in the adjoining figure. He can't measure this distance directly over the water. So, he selects the point S from where a straight line to point Q stays on land so he can mesure distance. he then moves eastward a distance of 400 m from point S to T , so that the line of sight from point T to P cuts the previous line SQ at R. finally with a long measuring tape. he determines that. SR = 250 m, QR= 1250 m
Determine if this is enough information to calculate the distance PQ and if so, find PQ and hence find the time taken by a swimmer to cross the river PQ with a uniform speed of 800 m/hr.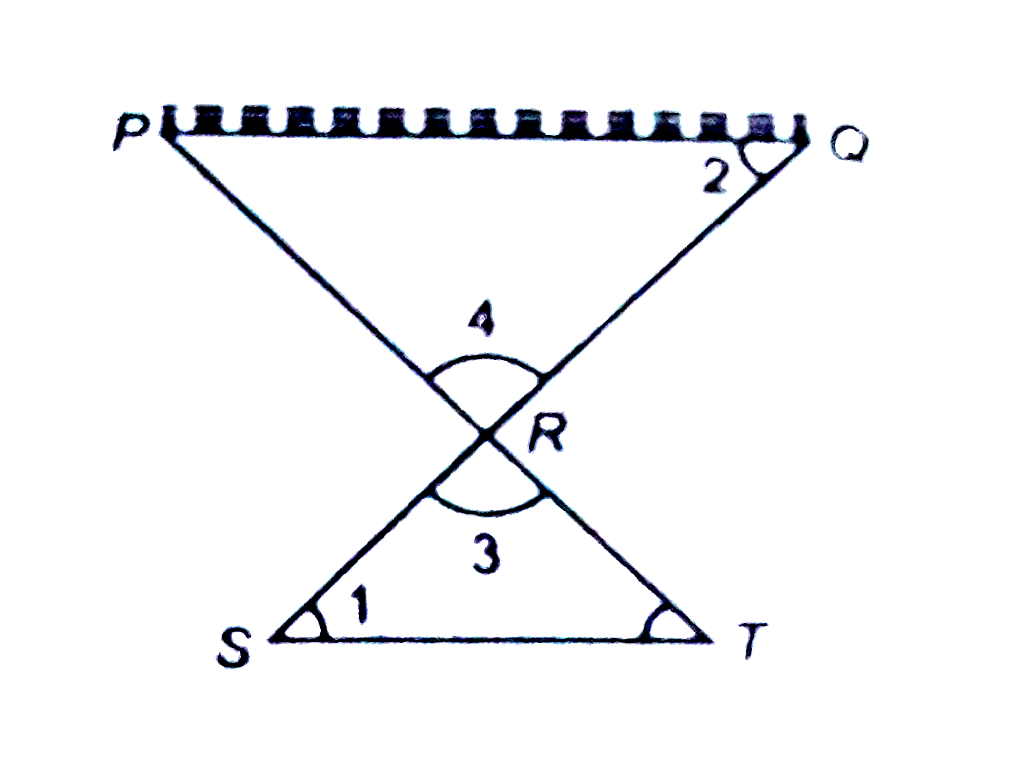
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View Solution

 .
.