The distance travelled by a falling body in the last second of its motion, to that in the last but one second is 7: 5, the velocity with which body strikes the ground is
19.6m/s
39.2m/s
29.4m/s
49m/s
The correct Answer is:B
To solve the problem, we need to find the velocity with which a falling body strikes the ground, given the ratio of distances traveled in the last second and the last but one second of its motion.
1. Understanding the Problem:
We are given that the distance traveled by a falling body in the last second of its motion (let's denote it as Sn) to that in the last but one second (denote it as Sn−1) is in the ratio 7:5.
2. Using the Formula for Distance:
The distance traveled in the nth second can be expressed as:
Sn=u+12g(n2)−(u+12g((n−1)2))=12g(2n−1)
Since the initial velocity u=0 for a freely falling body, we simplify this to:
Sn=12g(2n−1)
Similarly, for Sn−1:
Sn−1=12g(2(n−1)−1)=12g(2n−3)
3. Setting Up the Ratio:
Given the ratio SnSn−1=75:
12g(2n−1)12g(2n−3)=75
The 12g cancels out, leading to:
2n−12n−3=75
4. Cross-Multiplying:
Cross-multiplying gives:
5(2n−1)=7(2n−3)
Expanding both sides:
10n−5=14n−21
5. Rearranging the Equation:
Rearranging gives:
21−5=14n−10n
Thus:
16=4n⟹n=4
6. Finding the Final Velocity:
Now that we have n=4, we can find the final velocity v using the equation:
v=u+gt
Since u=0:
v=gt=g⋅4
Assuming g≈9.8m/s2:
v=9.8⋅4=39.2m/s
Final Answer:
The velocity with which the body strikes the ground is 39.2m/s.
We are given that the distance traveled by a falling body in the last second of its motion (let's denote it as Sn) to that in the last but one second (denote it as Sn−1) is in the ratio 7:5.
The distance traveled in the nth second can be expressed as:
Sn=u+12g(n2)−(u+12g((n−1)2))=12g(2n−1)
Since the initial velocity u=0 for a freely falling body, we simplify this to:
Sn=12g(2n−1)
Similarly, for Sn−1:
Sn−1=12g(2(n−1)−1)=12g(2n−3)
Given the ratio SnSn−1=75:
12g(2n−1)12g(2n−3)=75
The 12g cancels out, leading to:
2n−12n−3=75
Cross-multiplying gives:
5(2n−1)=7(2n−3)
Expanding both sides:
10n−5=14n−21
Rearranging gives:
21−5=14n−10n
Thus:
16=4n⟹n=4
Now that we have n=4, we can find the final velocity v using the equation:
v=u+gt
Since u=0:
v=gt=g⋅4
Assuming g≈9.8m/s2:
v=9.8⋅4=39.2m/s
The velocity with which the body strikes the ground is 39.2m/s.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Knowledge Check
The distance travelled by a body falling from reset in the frist, second and third seconds are in the ratio
A1:2:3B1:3:5C1:4:9Dnone of the aboveIn the given v-t graph the distance travelled by the body in 5 seconds will be
 A100 mB80 mC40 mD20 m
A100 mB80 mC40 mD20 m
The distance travelled by a body during last second of its total flight is d when the body is projected vertically up with certain velocity. If the velocity of projection is doubled, the distance travelled by the body during last second of its total flight is
View SolutionFor the velocity - time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the total distance covered by it in all the seven seconds
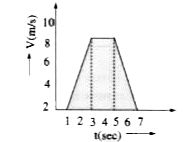
View SolutionThe distance travelled by a body during last second of its upward journey is d when the body is projected with certain velocity vertically up. If the velocity of projection is doubled, the distance travelled by the body during last second of its upward journey is
View SolutionA stone falls freely rest. The distance covered by it in the last second is equal to the distance covered by it in the first 2 s. The time taken by the stone to reach the ground is
View SolutionA stone falls freely such that the distance covered by it in the last second of its motion is equal to the distance covered by it in the first 5 seconds. It remained in air for :-
View SolutionFind the ratio of the distances travelled by a freely falling body in first, second and third second of its fall.
View Solution
