A ball is dropped from a height of 19.6 m above the ground. It rebounds from the ground and raises itself up to the sme height. Take the starting point s the origin and vertically downward as the positie X-axis. Draw approximate plots of x versus t, v versus t and a versus t. Neglect the small interval during which the ball was in contact with the ground.
Since the aceleration of theball during the cobtact is different from g, we have to treat the downward motion and the upward motion separately. For the downward motion a=g=9.8ms2,<br>x=ut+1/2 at^2=(4.9 m/s^2)t^2.<br>theballreachesthegroundwhenx=19.6m.thisgivest=2s.Aftertˆitmovesup,xdecreasesandatt=4s,xbecomeszero,theballreaχngthe∈itialp∮.<br>Wehavett=0,<br>,x=0<br>t=1,x=4.9m<br>t=2s,x=19.6m<br>t=3s,x=4.9m<br>t=4s,x=0.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C03_S01_020_S01.pngwh=80%mx-autosty≤=background:white;>.<br>Velocity:Dur∈gthefirsttwoseconds<br>v=u+at=(9.8 m/s^2)t<br>at t=0, v=0<br>at t=1s, v=9.8 m/s<br>att=2s,v=19.6ms
During the next two seconds the ball goes upwrd, velocity is negtive, magnitude decreasing and tat t=4,sv=0 Thus,
att=2,v=−19.6ms
at t=3s, v=-9.8 m/s
at t=4s, v=0

At t=2s there is an abrupt change in velocilty from 19.6 m,/s to -19.6 m/s In fasct this change in velocity takes plce over a small interval during which the ball remains in contact with the ground.
Acceleration: THe acceleration is constant 9.8ms2 throughtout the motion (except t t=2s). 
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Short Answer14videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 113videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises34videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
Similar Questions
A ball is dropped from a height h above ground,Neglect the air resistance,its velocity (v) varies with its height y above the ground as
View SolutionA ball is dropped from a height 20m above the ground and it rebounds with coefficient of restitution 0.5 The total time (in second) of motion of ball till it stops completely.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is dropped from a height h above ground. Neglect the air resistance, its velocity (v) varies with its height (y) above the ground as :-
A√2g(h−y)B√2ghC√2gyD√2g(h+y) - Question 2 - Select One
A ball is dropped from a height 100 m on the ground. If the coefficient of restitution is 0.2, the height to which the ball will go up after it rebounds for the IInd time.
A16 mB1.6 cmC1.6 mD16 cm - Question 3 - Select One
v34
A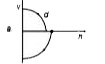 B
B C
C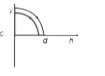 D
D
A ball is dropped vertically from a height d above the ground. It hits the ground and bounces up vertically to a height d/2. Neglecting the subsequent motion and the air resistance, how its velocity v varies with the height h above the ground?
View SolutionA ball is dropped vertically from a height d above the ground. It hits the ground and bounes up vertically to a height d/2. Neglecting subsequent motion and air resistance, its speed v varies with the height h above the ground as
View SolutionA ball is dropped from a height. If it takes 1s to cross the last 55m before hitting the ground, find the height from which it was dropped.
View SolutionA ball of mass 0.15kg is dropped from a height 10m strikes the ground and rebounds to the same height. The magnitude of impulse imparted to the ball is (g=10ms2) nearly:
View SolutionA ball is dropped from a height H above the ground. It hits the ground and bounces up vertically to a height H2 where it is caught. Taking origin at the point from where the ball was dropped, plot the variation of its displacement vs velocity. Take vertically downward direction as positive.
View Solution

