A vector →A makes an angle of 20∘and→B makes an angle of −−→110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
The correct Answer is:A, C
To find the resultant of the two vectors →A and →B, we will follow these steps:
Step 1: Identify the Magnitudes and Angles
- The magnitude of vector →A is 3m and it makes an angle of 20∘ with the X-axis.
- The magnitude of vector →B is 4m and it makes an angle of 110∘ with the X-axis.
Step 2: Calculate the Components of Each Vector
We can express each vector in terms of its components along the X and Y axes.
For vector →A:
- Ax=Acos(20∘)=3cos(20∘)
- Ay=Asin(20∘)=3sin(20∘)
For vector →B:
- Bx=Bcos(110∘)=4cos(110∘)
- By=Bsin(110∘)=4sin(110∘)
Step 3: Calculate the Components
Using trigonometric values:
- cos(20∘)≈0.9397
- sin(20∘)≈0.3420
- cos(110∘)≈−0.3420
- sin(110∘)≈0.9397
Now substituting these values:
- Ax=3×0.9397≈2.8191m
- Ay=3×0.3420≈1.0260m
- Bx=4×(−0.3420)≈−1.3680m
- By=4×0.9397≈3.7588m
Step 4: Find the Resultant Components
Now, we can find the components of the resultant vector →R:
- Rx=Ax+Bx=2.8191−1.3680≈1.4511m
- Ry=Ay+By=1.0260+3.7588≈4.7848m
Step 5: Calculate the Magnitude of the Resultant Vector
The magnitude of the resultant vector →R can be calculated using the Pythagorean theorem:
R=√R2x+R2y
Substituting the values:
R=√(1.4511)2+(4.7848)2≈√2.1077+22.9119≈√25.0196≈5.0m
Step 6: Conclusion
The magnitude of the resultant vector →R is approximately 5.0m.
---
- The magnitude of vector →A is 3m and it makes an angle of 20∘ with the X-axis.
- The magnitude of vector →B is 4m and it makes an angle of 110∘ with the X-axis.
We can express each vector in terms of its components along the X and Y axes.
- Ax=Acos(20∘)=3cos(20∘)
- Ay=Asin(20∘)=3sin(20∘)
- Bx=Bcos(110∘)=4cos(110∘)
- By=Bsin(110∘)=4sin(110∘)
Using trigonometric values:
- cos(20∘)≈0.9397
- sin(20∘)≈0.3420
- cos(110∘)≈−0.3420
- sin(110∘)≈0.9397
- Ax=3×0.9397≈2.8191m
- Ay=3×0.3420≈1.0260m
- Bx=4×(−0.3420)≈−1.3680m
- By=4×0.9397≈3.7588m
Now, we can find the components of the resultant vector →R:
- Rx=Ax+Bx=2.8191−1.3680≈1.4511m
- Ry=Ay+By=1.0260+3.7588≈4.7848m
The magnitude of the resultant vector →R can be calculated using the Pythagorean theorem:
R=√R2x+R2y
Substituting the values:
R=√(1.4511)2+(4.7848)2≈√2.1077+22.9119≈√25.0196≈5.0m
The magnitude of the resultant vector →R is approximately 5.0m.
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 2
5 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
Similar Questions
A vector →A and →B make angles of 20∘ and 110∘ respectively with the X-axis. The magnitudes of these vectors are 5m and 12m respectively. Find their resultant vector.
View SolutionLet →Aand→B be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angles 30∘and60∘ respectively, find the resultant.
View Solution
Knowledge Check
A vector a makes 30∘ and b makes 120∘ angle with the x-axis. The magnitude of these vectors are 3 unit and 4 unit, respectively. The magnitude of resultant vector is
A3 unitB4 unitC5 unitD1 unitTwo vectors →Aand→B inclined at an angle θ have a resultant →R which makes an angle α with →A and angle β with →B. Let the magnitudes of the vectors →A,→Band→R be represented by A, B and R respectively. Which of the following relations is not correct ?
ARsin(α+β)=Asinα=BsinβBRsinα=Bsin(α+β)CAsinα=BsinβDRsinβ=Asin(α+β)A vector of magnitude 14 lies in the xy-plane and makes an angle of 60∘ with x -axis . The components of the vector in the direction of x -axis and y-axis are
A7,7√3B7√3,7C14√3,14/√3D14/√3,14√3
A vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
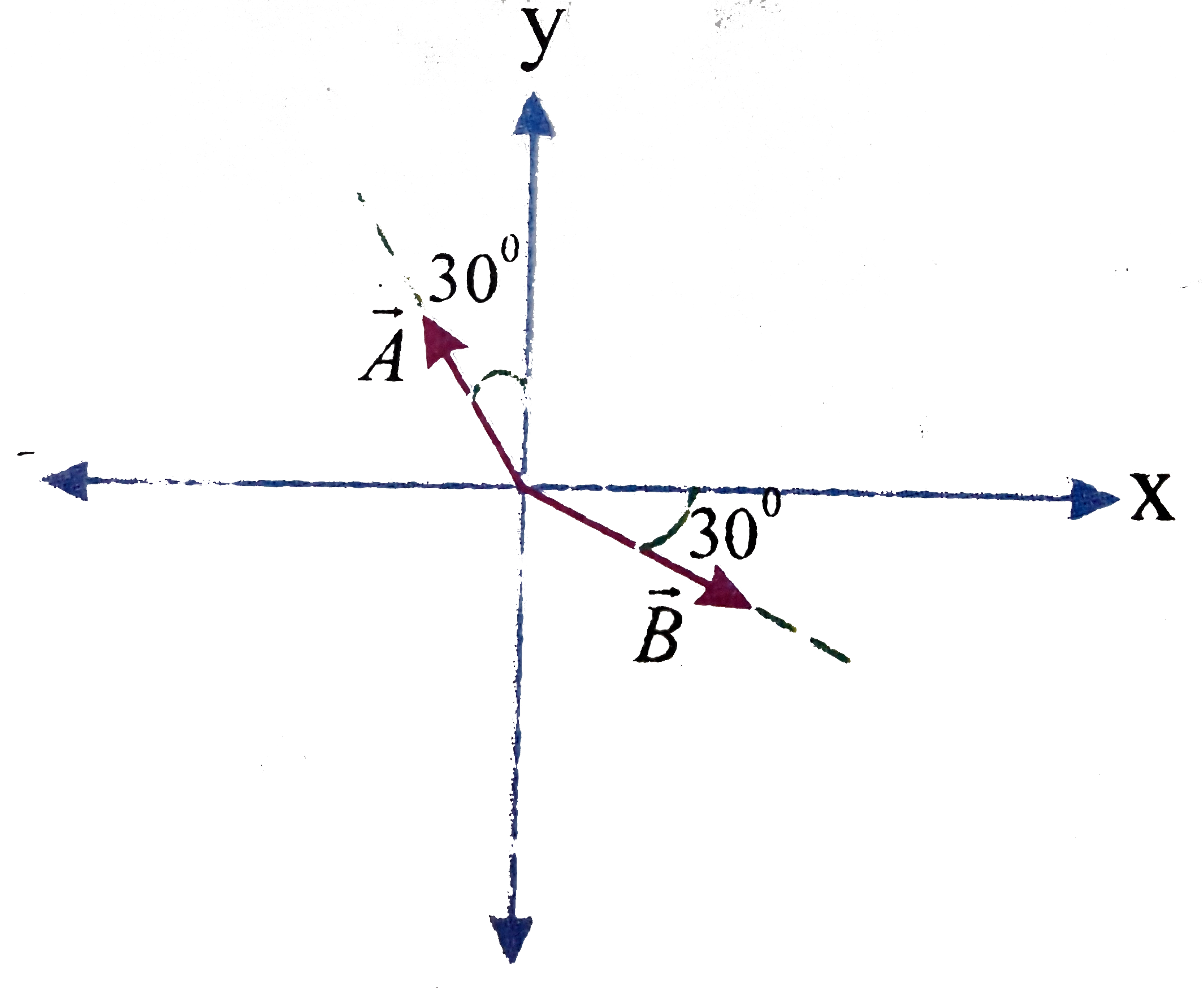
View SolutionA vector →A makes an angle 30∘ with the Y-axis in anticlockwise direction. Another vector →B makes an angle 30∘ with the x-axis in clockwise direction. Find angle between vectors →A and →B.
View SolutionA vector makes an angle of π4 with each of x-axis and y-axis Find the angle made by it with the z-axis.
View SolutionThe resultant of →Aand→B makes an angle alpha with →A and βand→B,
View SolutionThe resultant of →A and →B makes an angle α with →Aand→β with →B, then -
View Solution
