A ball is dropped from a height of 320m above the ground. After every collision, the speed of ball decreases by 50%. Taking dropping point as origin, downward direction positive and collision time negligible, sketch the v-t, s-t and a-t graphs. Also calculate the total distance traveled by the ball and the total time of journey.
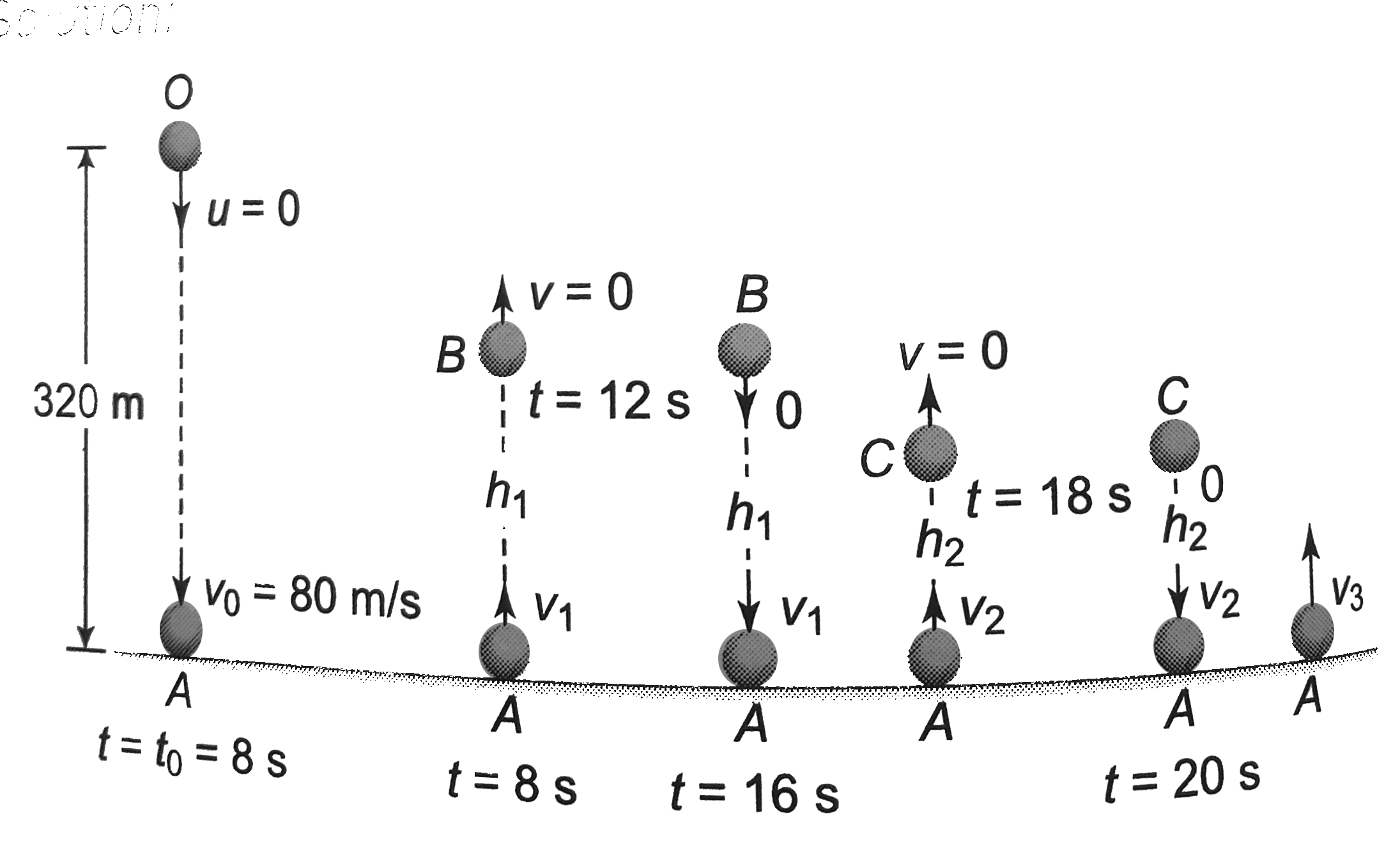
O to A: s=ut+12gt2
320=0+12×10×t20⇒t0=8s
v=u+gt
v0=0+10t0=80m/s
Speed of the ball after first collision =12(80)=40m/s=v1
A to B: 0=v21−2gh1⇒0=(40)2−20h1⇒h1=80m
0=v1−gt1⇒0=40−10t1⇒t1=4s
Speed of the ball after second collision=12×40.....=20m/s=v2
A to C: 0=v22−2gh2⇒0=(20)2−2×10×h2⇒h2=20m
0=v2−gt2⇒0=20−10t2⇒t2=2s
and so on.
After every collision, the speed becomes half, the maximum height becomes 1/4th and the time to reach at the highest point becomes half.
Topper's Solved these Questions
Similar Questions
A particle is dropped from the top of a tower of height 80 m. Assuming the dropping point as the origin and the downward direction position, sketch v-t, s-t and a-t graph. (g=10m/s2)
View SolutionA ball is dropped from a height of 19.6 m above the ground. It rebounds from the ground and raises itself up to the sme height. Take the starting point s the origin and vertically downward as the positie X-axis. Draw approximate plots of x versus t, v versus t and a versus t. Neglect the small interval during which the ball was in contact with the ground.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is dropped from a 10 m height. How much time, it will take to reach the ground ?
A1.41 sB0.58 sC2.34 sDnone of these - Question 2 - Select One
A ball is dropped from a 10 m height ,How much time , it will take to reach the ground ?
A1.41 sB0.58 sC2.34 sDNone of these - Question 3 - Select One
A ball is dropped from a height of 10 m. If the energy of the ball reduces by 40% after striking the ground, how much high can the ball bounce back ? (g=10m/s2)
A4 mB8 mC6 mD5 m
A ball is dropped from a height 20m above the ground and it rebounds with coefficient of restitution 0.5 The total time (in second) of motion of ball till it stops completely.
View SolutionA ball is dropped from a height of 80 m on a floor. At each collision, the ball loses half of its speed. Plot the speed-time graph and velocity-time graph of its motion till two collisions With the floor. [Take g=10m/s2]
View SolutionA ball is dropped from a height 64 m above the ground and every time it hits the ground it rises to a height equal to half of the previous height. The height attained after it hits the ground for the 16h time is
View SolutionA ball is dropped from a height of 80 in. The distance travelled by it in the fourth second will be_____ (take g=10m/s2)
View SolutionA ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View Solution

