A ball is given velocity $u = \sqrt{3 g d}$ at an angle $45^{\circ}$ with horizontal. It strikes a wall at distance $d$ and returns to its original position. Find the coefficient of restitution $e$ .

Text Solution

Verified by Experts

The velocity remains same in the vertical direction (along the surface) and the velocity becomes $e$ times and opposite in the horizontal direction ( $⊥^{a r}$ to the surface)
Time from O to $A_{1}, t_{1} = \frac{d}{u {cos 45}^{\circ}}$ (uniform motion) Time from A to $O, t_{2} = \frac{d}{e u {cos 45}^{\circ}}$
Total time $t = t_{1} + t_{2} = \frac{d}{u {cos 45}^{\circ}} (1 + \frac{1}{e})$
Time for vertical motion (O to O)
$0 = u {sin 45}^{\circ} T - \frac{1}{2} g T^{2} \Rightarrow T = \frac{2 u {sin 45}^{\circ}}{g}$
$t = T$
$\frac{d}{u {cos 45}^{\circ}} (1 + \frac{1}{e}) = \frac{2 u {sin 45}^{\circ}}{g}$
$d (1 + \frac{1}{e}) = \frac{2 u^{2} {sin 45}^{\circ} {cos 45}^{\circ}}{g}$
$= \frac{u^{2}}{g} {sin 90}^{\circ} = \frac{3 g d}{g} = 3 d$
$1 + \frac{1}{e} = 3 \Rightarrow \frac{1}{e} = 2 \Rightarrow e = \frac{1}{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A ball is projected at $t = 0$ with velocity $v_{0}$ at angle $θ$ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
ABall will return to ground at $t = \frac{2 v_{0} sin θ}{g}$
B $d = e (R - L) (where R is \frac{v_{0} sin 2 θ}{g})$
Cmaximum height during motion $= \frac{v_{0}^{2} {sin}^{2} θ}{2 g}$
Dit will return to ground at $t < \frac{2 v_{0} sin θ}{g}$
Question 2 - Select One
A ball of mass $m$ is projected with a velocity $' u'$ at angle $θ$ with the horizontal. It collides with a smooth box of mass $' M'$ at its highest position. If the co-efficient of restitution is $' e'$ .

Find the horizontal distance travelled by the ball before collision.
A $\frac{u^{2} 2 sin θ cos θ}{g}$
B $\frac{u^{2} sin θ cos θ}{g}$
C $\frac{u^{2} sin θ cos θ}{2 g}$
D $\frac{u^{2} sin θ cos θ}{4 g}$
Question 3 - Select One
A ball of mass $m$ is projected with a velocity $' u'$ at angle $θ$ with the horizontal. It collides with a smooth box of mass $' M'$ at its highest position. If the co-efficient of restitution is $' e'$ .

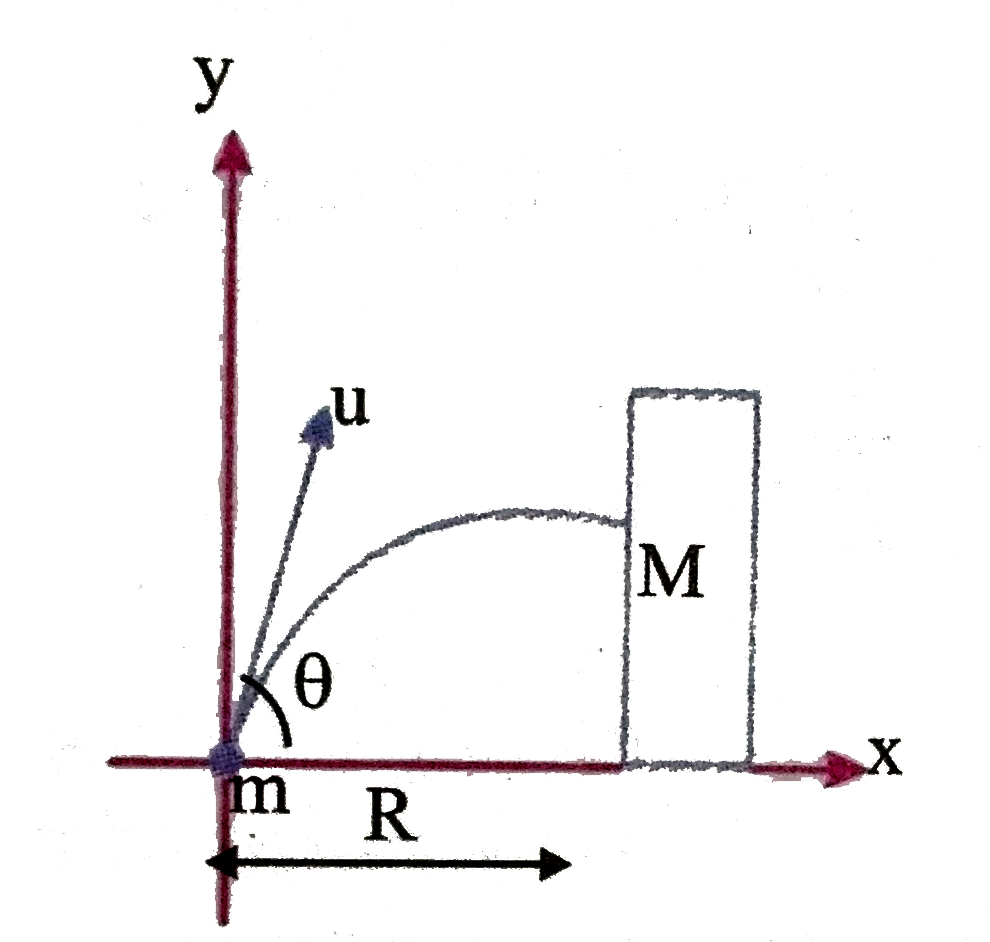
FInd the velocity of the ball after collision
A $(\frac{m - e M}{M + m}) u cos θ$
B $(\frac{M - e m}{M + m}) u cos θ$
C $(\frac{m + e M}{M + m}) u sin θ$
D $(\frac{m - e M}{M + m}) u sin θ$

CP SINGH-CENTER OF MASS-Exercises

Home
Ask Doubt
Profile