A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.

Find the position at which the ball meets the x-axis from the origin
(M(1−e)+2mM+m)R
(m(1−e)+2MM+m)R
(M+m(1−e)M+m)R
(M(1−e)+2m2(M+m))R
The correct Answer is:A

Recoil velocity of ball after collision v(m−eMM+m)ucosθ
From v1=(M1−eM2M1+m2)+2m2u2m1+m2
R'R=vucosθ=(eM−mM+m),R'=(eM−mM+m)R
The ball hit at a point 'P' at a distance
Δx=R−R'=R(1−(eM−mM+m))
=R(M(1−e)+2mM+m)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Subjective type Questions9videos
COLLISION
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-I (H.W)52videos
COLLISION
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Multiple Answer11videos
COLLISION
- BOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)51videos
CIRCULAR MOTION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
Similar Questions
A particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View Solution
Knowledge Check
- Question 1 - Select One
A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
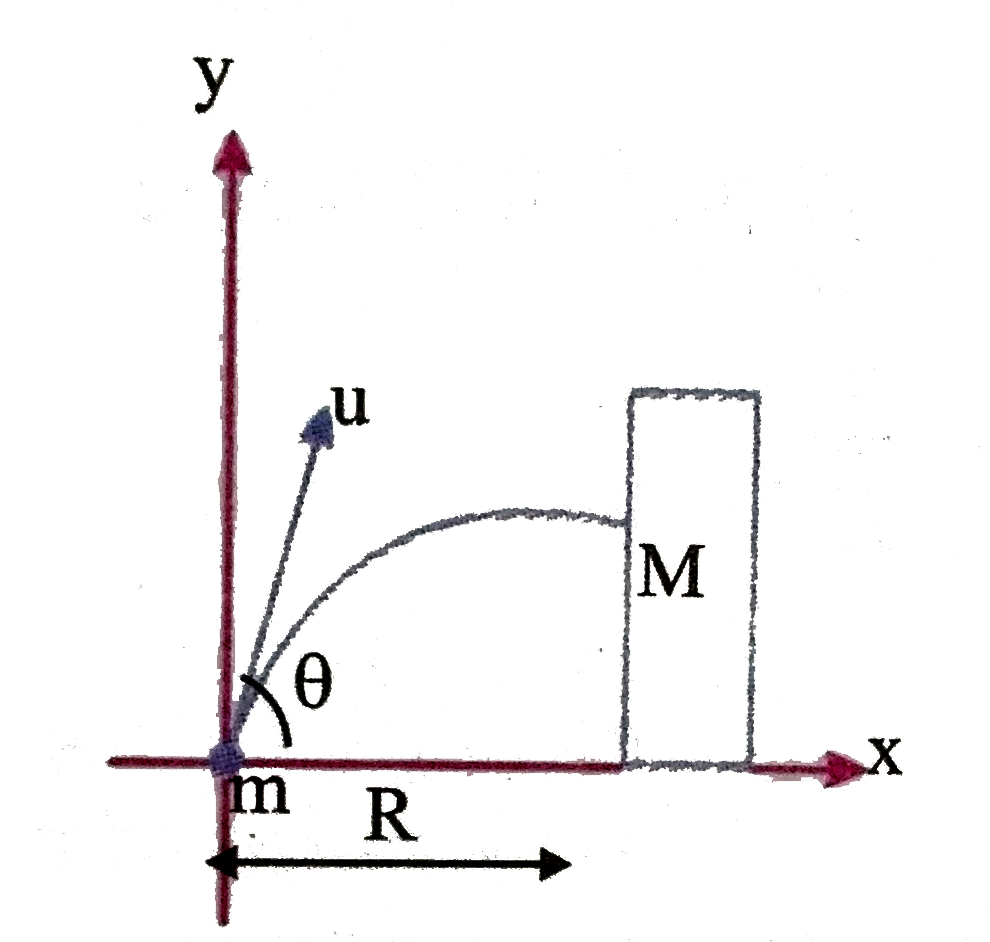
FInd the velocity of the ball after collisionA(m−eMM+m)ucosθB(M−emM+m)ucosθC(m+eMM+m)usinθD(m−eMM+m)usinθ - Question 2 - Select One
A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.

Find the horizontal distance travelled by the ball before collision.Au22sinθcosθgBu2sinθcosθgCu2sinθcosθ2gDu2sinθcosθ4g - Question 3 - Select One or More
A ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
ABall will return to ground at t=2v0sinθgBd=e(R−L)(whereRisv0sin2θg)Cmaximum height during motion =v20sin2θ2gDit will return to ground at t<2v0sinθg
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA ball is given velocity u=√3gd at an angle 45∘ with horizontal. It strikes a wall at distance d and returns to its original position. Find the coefficient of restitution e.
View SolutionA particle of mass m projected horizontally with velocity u. if it makes an angle θ with the horizontal after some time, then at that instant, its be Broglie wavelength is
View SolutionA ball is projecte with a velocity 20ms−1 at an angle to the horizontal. In order to have the maximum range. Its velocity at the highest position must be
View SolutionA ball is projected with initial velocity u at an angle θ to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :
 View Solution
View Solution

