A ball is thrown vertically upwards with a velocity of $20 m s^{- 1}$ from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take $g = 10 m s^{- 2}$ . Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

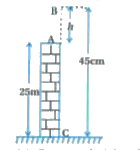
(a) Suppose height of multistorey building is d = 25 m
Initial velocity of ball thrown upwards from point A,
$v_{0} = 20 m s^{- 1}$
Acceleration $a = g = - 10 m s^{- 2}$
Final velocity at point B, $v = 0 m s^{- 1}$
Suppose, ball covers height h from A to B,
From third equation of motion,
$v^{2} - v_{0}^{2} = 2 a h$
$∴ 0 - {(20)}^{2} = 2 (- 10) \times h$
$∴ - 400 = - 20 h$
$∴ h = 20 m$
Bal will rise upto 20 m from top building
(b) Total time of flight of ball can be find out in two parts,
(i) $t_{1}$ is time taken to rise from A to B and
(ii) $t_{2}$ is time taken to fall from B to C.
$∴ (i)$ From first equation of motion.
$A B = 20 c m$
In $v = v_{0} + a t, v = 0 and v_{0} = 20 m / s,$
$a = - 10 m / s^{2}, 0 = 20 - 10 t_{1}, t = t_{1}$
$∴ t_{1} = 2 s ... (1)$
(ii) Now $B C = 20 + 25 = 45 m,$ time taken to cover it is $t_{2},$
$S = v_{0} t \frac{1}{2} a t^{2}$
$S = B C = 45 m, a = - 10 m s^{- 2}$
$∴ - 45 = 0 \times t_{2} + \frac{1}{2} \times (- 10) t_{2}^{2}$
$∴ - 45 = - 5 t_{2}^{2}$
$∴ t_{2}^{.2} = 9$
$∴ t_{2} = 3 s ... (2)$
$∴$ Total time of flight,
$t = t_{1} + t_{2}$
$t = 2 + 3$
[From equation (1) and (2)]
$t = 5 s$
(b) Second method: Total time can be determined from initial final positions of ball with respect to origin.
From equation of motion,
$y = y_{0} + v_{0} t + \frac{1}{2} a t^{2}$
$y_{0} = 25 m, v_{0} = 20 m s^{- 1}, y = 0 m$
$a = - 10 m s^{- 2}$
$∴ 0 = 25 + 20 t + \frac{1}{2} (- 10) t^{2}$
$∴ 5 t^{2} = 25 + 20 t$
$∴ 5 t^{2} - 20 t - 25 = 0$
$∴ t^{2} - 4 t - 5 = 0$
$∴ (t - 5) (t + 1) = 0$
$∴ t - 5 = 0 or t + 1 = 0$
$∴ t = 5 s or t = - 1 s$ which is impossible.
$∴ t = 5 s$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-MOTION IN A STRAIGHT LINE -SECTION-B

Home
Ask Doubt
Profile