A ball of a mass m is connected to two rubber bands of length L, each under tension T as shown in figure . The ball is displaced by a small distance y perpendicular to the length of the rubber band. Assuming the tension does not change , shown that (a) the restoring force is −(2T/L)y and (b) the system exhibits simple harmonic motion with an angular frequency ω=√2T/mLs.

a. If we displace the block upward the net tension towards mean position will proved the restoration force on the block.
∑¯¯¯F=−2Tsinθ, where θ=tan−1(y/L)
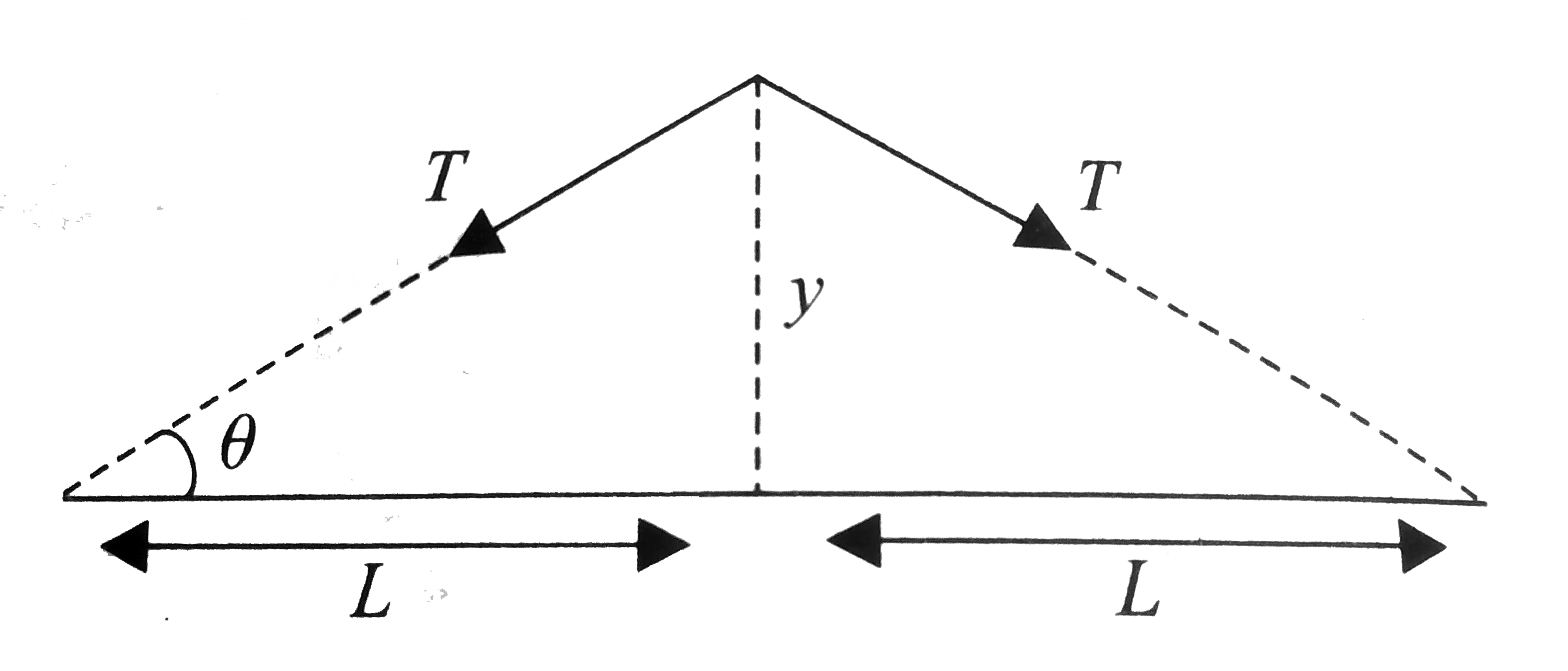
Since for a small displacement.
sinθ=tanθ=yL
and the resultant is
∑¯¯¯F=(−2TyL)
b. Since there is a restoring force that is proportional to the position , it cause the system to move with simple harmonic motion like a block-spring system . Thus, we can think of
ω=√km=sqer(2TmL)
Not enything with a stable equilirium position will exercute simple harmonic motion when disturb and released, but a lot of things do when the disturbance is small.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A ball of a mass m is connected to two rubber bands of length L, each under tension T as shown in figure . The ball is displaced by a small distance y perpendicular to the length of the rubber band. Assuming the tension does not change , shown that (a) the restoring force is −(2T/L)y and (b) the system exhibits simple harmonic motion with an angular frequency ω=√2T/mLs.

View SolutionThe tension T in the string shown in figure is

View Solution
Knowledge Check
Find the tension T2 in the system shown in the figure.
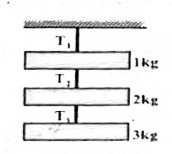 A1gNB2gNC5gND6gN
A1gNB2gNC5gND6gNFind the tension T2 in the system shown in fig
 A1g NB2g NC5g ND6g N
A1g NB2g NC5g ND6g NFind the tension T2 in the system shown in fig.
 A1g NB2g NC5g ND6g N
A1g NB2g NC5g ND6g N
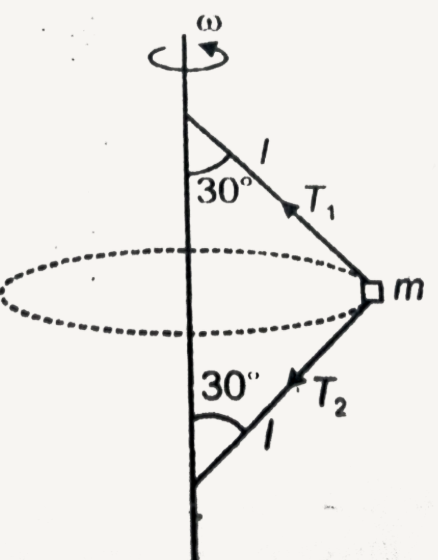
A particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals ω, then
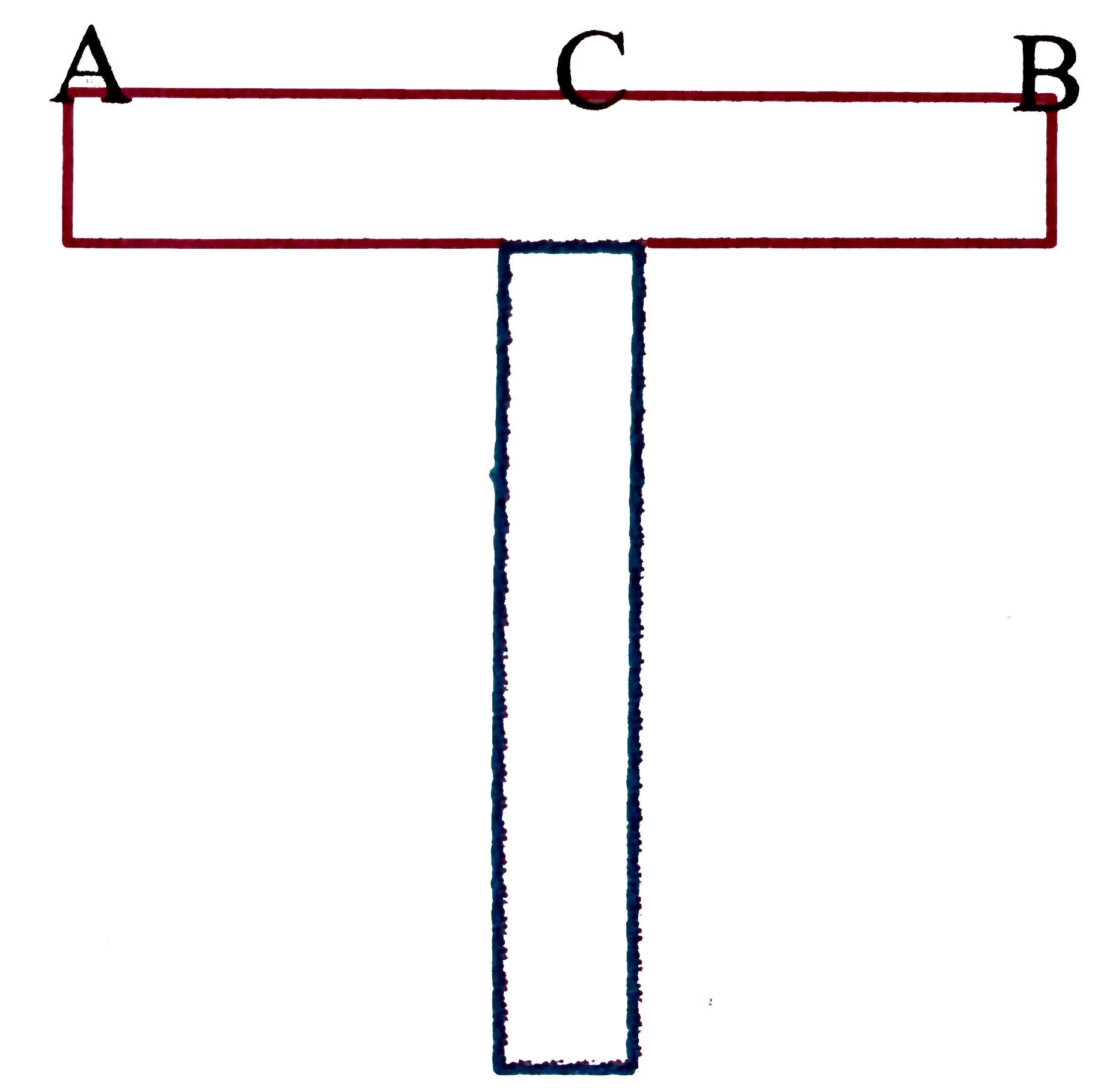
View SolutionTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
View SolutionA rod of length L and mass M is acted on by two unequal forces F1 and F2(<F)as shown in the figure.
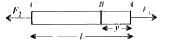
The tension in the rod at a distance y from the end A is given by
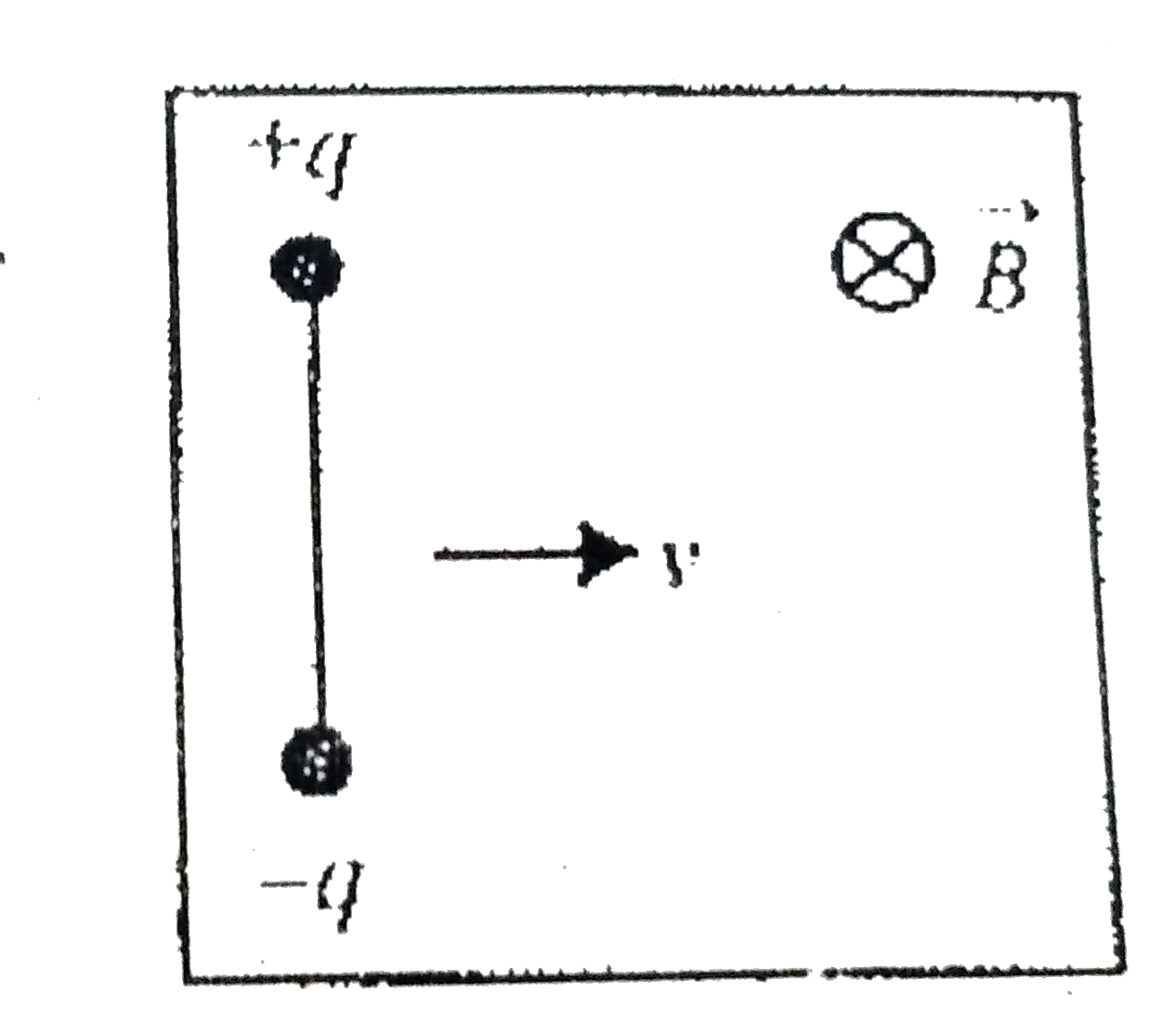
View SolutionTwo changes +q and -q are attached to the two end of a light rod of length L, as shown in figure . The system is given a velocity v perpendicular to magnetic force on the system of charges and magnitude of force on one charges by the rod , are respectively .
View SolutionA rubber band of length l has a stone of mass m tied to its one end. It is whirled with speed v so that the stone describes a horizontal circular path. The tension T in the rubber band is -
View Solution
