A rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

The correct Answer is:12π√3k27M+7m
At equlibrium position deformation of the spring is x0
kx0=14=Mg(34l)+mg(14)
When the rod is further rotated through an angle θ from equlibrium position, the restoring tarque.
τ=−[k(x+x0)14cosθ−Mg(34)Lcosθ]−mg(L4)cosθ
=−[k(x+x0)14−Mg(34)L−mg(L4)]cosθ
For small θ,cosθ≈1
τ=−kl4x ⇒lα=−kl24θ
l=m(34L)2+mL212+m(L4)2
f=12π√3k27M+7m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct107videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.223videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
From the given figure find the frequency of oscillation of the mass m
 An=12π√KmBn=12π√K22mCn=2π√m2KDn=12n√K2m
An=12π√KmBn=12π√K22mCn=2π√m2KDn=12n√K2m - Question 2 - Select One
A thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23m - Question 3 - Select One
A rod is hinged vertically at one end and is forced to oscillate in a vertical plane with hinged end at the top, the motion of the rod:
Ais simple harmonicBis oscillatory but not simple harmonicCis pericolic but not oscillatoryDmay be simple harmonic
An L-shaped bar of mass M is pivoted at one of its end so that it can freely rotate in a vertical plane, as shown in the figure
a. Find the value of θ0 at equilibrium
b. If it is slightly displacement from its equilibrium position, find the frequency of oscillation.
 View Solution
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
 View Solution
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 View Solution
View SolutionA uniform semi circular ring of radius R and mass m is free to oscillate about its one end in its vertical plane as shown in the figure. Find time period of SHM of its centre of mass of the ring (take π2=10)
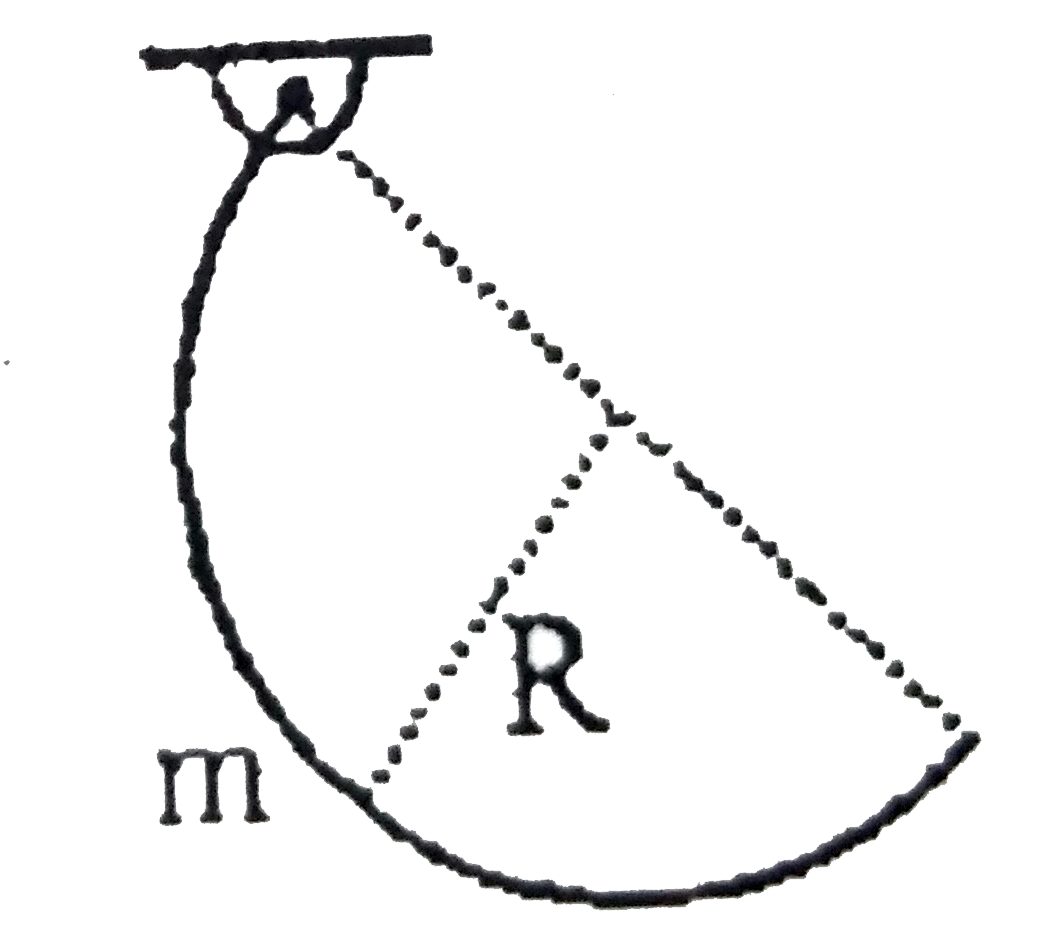 View Solution
View SolutionA uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-
 View Solution
View Solution



