A ball of mass 0.6kg attached to a light inextensible string rotates in a vertical circle of radius 0.75m such that it has speed of 5ms−1 when the string is horizontal. Tension in the string when it is horizontal on other side is (g=10ms−2).
To find the tension in the string when the ball is at the horizontal position in a vertical circular motion, we can follow these steps:
1. Identify the Given Values:
- Mass of the ball, m=0.6kg
- Radius of the circle, r=0.75m
- Speed of the ball, v=5m/s
- Acceleration due to gravity, g=10m/s2
2. Understand the Forces Acting on the Ball:
- When the ball is at the horizontal position, the forces acting on it are:
- The tension T in the string acting towards the center of the circle.
- The weight of the ball mg acting downwards.
3. Use the Centripetal Force Equation:
- At the horizontal position, the centripetal force required to keep the ball moving in a circle is provided entirely by the tension in the string since the weight does not contribute to the centripetal force at this position.
- The centripetal force Fc is given by:
Fc=mv2r
4. Calculate the Centripetal Force:
- Substituting the values into the centripetal force equation:
Fc=0.6×(5)20.75
- Calculate (5)2=25:
Fc=0.6×250.75
- Calculate 0.6×25=15:
Fc=150.75
- Calculate 150.75=20:
Fc=20N
5. Conclusion:
- The tension in the string when the ball is horizontal is T=20N.
Final Answer:
The tension in the string when it is horizontal is 20N.
---
- Mass of the ball, m=0.6kg
- Radius of the circle, r=0.75m
- Speed of the ball, v=5m/s
- Acceleration due to gravity, g=10m/s2
- When the ball is at the horizontal position, the forces acting on it are:
- The tension T in the string acting towards the center of the circle.
- The weight of the ball mg acting downwards.
- At the horizontal position, the centripetal force required to keep the ball moving in a circle is provided entirely by the tension in the string since the weight does not contribute to the centripetal force at this position.
- The centripetal force Fc is given by:
Fc=mv2r
- Substituting the values into the centripetal force equation:
Fc=0.6×(5)20.75
- Calculate (5)2=25:
Fc=0.6×250.75
- Calculate 0.6×25=15:
Fc=150.75
- Calculate 150.75=20:
Fc=20N
- The tension in the string when the ball is horizontal is T=20N.
The tension in the string when it is horizontal is 20N.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Solved Examples
Explore 2 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Miscellaneous Examples
Explore 5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionA body is moving in a vertical circle of radius r such that the string is just taut at its highest point. The speed of the particle when the string is horizontal is
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
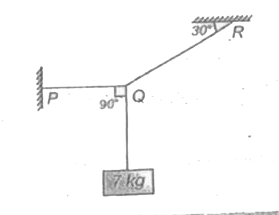
View SolutionA particle is rotated in vertical circle by connecting it to string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA particle of mass 100 g, is made to describe a vertical circle of radius 1 m. Its instantaneous speed is 1ms−1 when the string makes an sngle of 30∘ with the vertical Find the tension in the string at this position. Can the particle complete its circular path? (g=10ms−2)
View SolutionA particle is rotated in verticla circle by connecting it to string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA stone of mass 1 kg tied at the end of a string of length 1 m and is whirled in a verticle circle at a constant speed of 3ms−1. The tension in the string will be 19 N when the stone is (g=10ms−1)
View SolutionAn object of mass 10kg is attached to roof by string whirled round a horizontal circle of radius 4 and 30∘ to the vertical. The tension in the string (approximately) is
View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
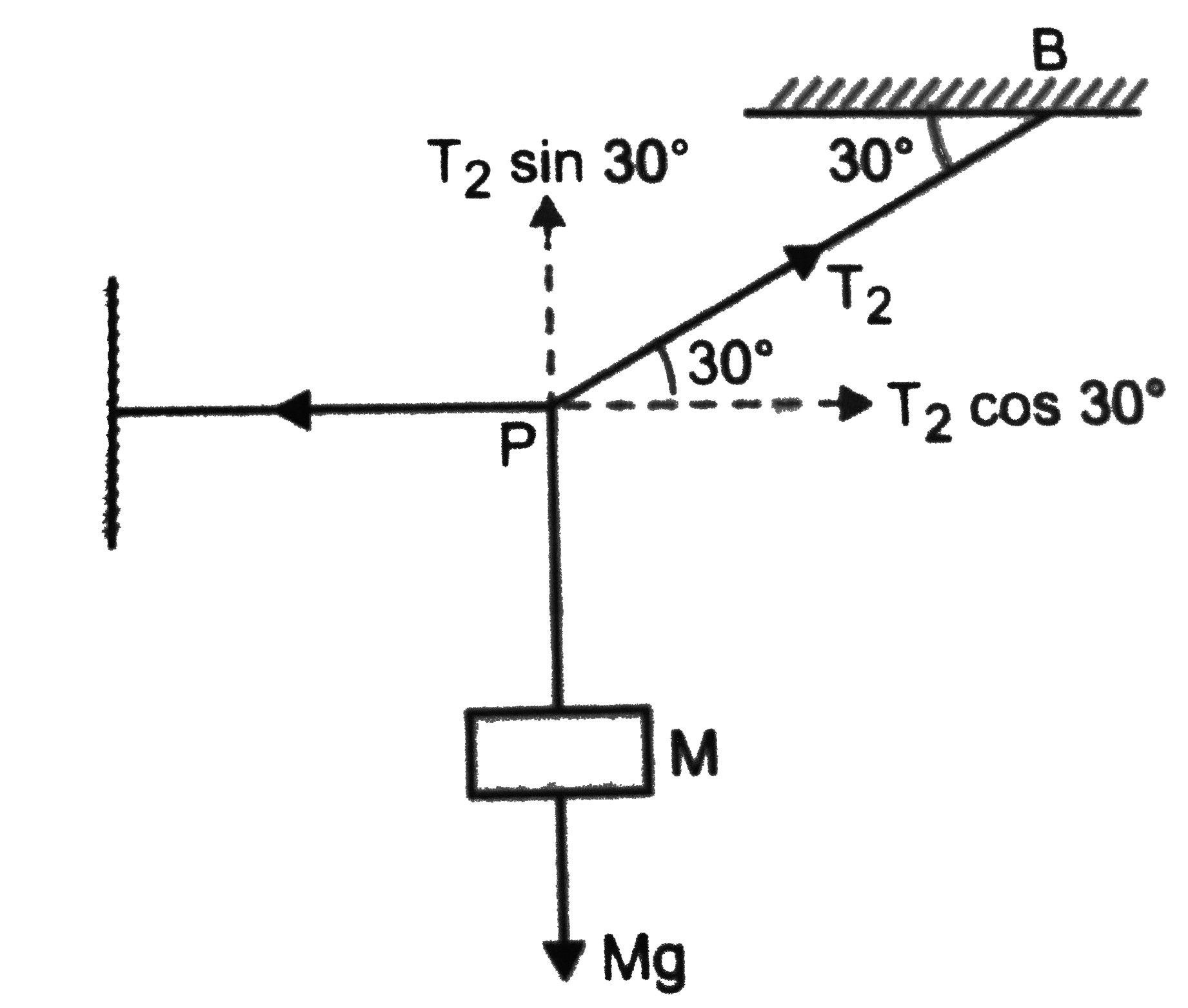
View Solution